Регистрация Спросить otvet5GPT
577656
21.02.2023 14:34
Математика
Есть ответ 👍

|-у|=1. |х|=0 -|a|=5 решите уравнение с модулем

208
435
Посмотреть ответы 2

Ответы на вопрос:

PROматематик
PROматематик
4,6(51 оценок)
Y=-1 x=0 a=-5 xtdtcgcxcgfvfht
хорошистка552
хорошистка552
4,5(74 оценок)

1.

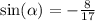
\sin( \alpha ) = - \frac{8}{17} \\

угол принадлежит 4 четверти, значит косинус положительный, тангенс и котангенс отрицательные.

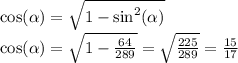
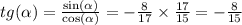
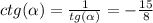
\cos( \alpha ) = \sqrt{1 - { \sin}^{2} (\alpha )} \\ \cos( \alpha ) = \sqrt{1 - \frac{64}{289} } = \sqrt{ \frac{225}{289} } = \frac{15}{17}

tg( \alpha ) = \frac{ \sin( \alpha ) }{ \cos( \alpha ) } = - \frac{8}{17} \times \frac{17}{15} = - \frac{8}{15} \\

ctg( \alpha ) = \frac{1}{tg( \alpha )} = - \frac{15}{8} \\

2.

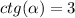
ctg (\alpha ) = 3

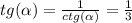
tg( \alpha ) = \frac{1}{ctg( \alpha )} = \frac{1}{3} \\

угол принадлежит 3 четверти => синус и косинус отрицательные.

по формуле:

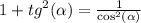
1 + {tg}^{2} ( \alpha ) = \frac{1}{ { \cos }^{2}( \alpha ) } \\

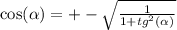
\cos( \alpha ) = + - \sqrt{ \frac{1}{1 + {tg}^{2}( \alpha ) } } \\

знак зависит от угла

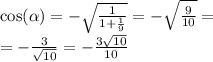
\cos( \alpha ) = - \sqrt{ \frac{1}{1 + \frac{1}{9} } } = - \sqrt{ \frac{9}{10} } = \\ = - \frac{3}{ \sqrt{10} } = - \frac{3 \sqrt{10} }{10}

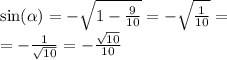
\sin( \alpha ) = - \sqrt{1 - \frac{9}{10} } = - \sqrt{ \frac{1}{10} } = \\ = - \frac{1}{ \sqrt{10} } = - \frac{ \sqrt{10} }{10}

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS