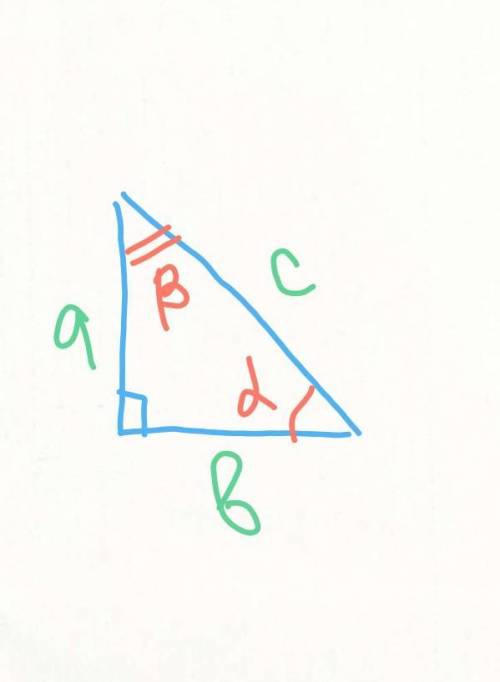
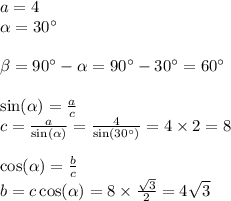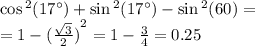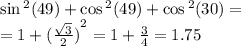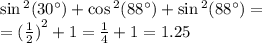Точка м не принадлежит плоскости треугольника авс .каково распложение мс и ав?

137

383

Посмотреть ответы 2

Ответы на вопрос:

milana0512

Геометрия

4,7(69 оценок)

прямая ab лежит в плоскости (авс), так как 2 её точки в и с лежат в плоскости (авс). прямая ам пересекает плоскость (авс) в точке а, не лежащей на ab, значит mc и ab скрещивающиеся прямые.

martynovich04

Геометрия

4,8(69 оценок)

$a = 4 \\ \alpha = 30^{\circ} \\ \\ \beta = 90^{\circ} - \alpha = 90^{\circ} - 30^{\circ} = 60^{\circ} \\ \\ \sin( \alpha ) = \frac{a}{c} \\ c = \frac{a}{ \sin( \alpha ) } = \frac{4}{ \sin(30^{\circ} ) } = 4 \times 2 = 8 \\ \\ \cos( \alpha ) = \frac{b}{c} \\ b = c \cos( \alpha ) = 8 \times \frac{ \sqrt{3} }{2} = 4 \sqrt{3}$

$\cos {}^{2} (17^{\circ} ) + \sin {}^{2} (17^{\circ} ) - \sin {}^{2} (60) = \\ = 1 - {( \frac{ \sqrt{3} }{2} )}^{2} = 1 - \frac{3}{4} = 0.25$

$\sin {}^{2} (49) + \cos {}^{2} (49) + \cos {}^{2} (30) = \\ = 1 + {( \frac{ \sqrt{3} }{2} )}^{2} = 1 + \frac{3}{4} = 1.75$

$\sin {}^{2} (30^{\circ} ) + \cos {}^{2} (88^{\circ} ) + \sin {}^{2} (88^{\circ} ) = \\ = {( \frac{1}{2}) }^{2} + 1 = \frac{1}{4} + 1 = 1.25$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.