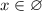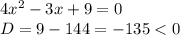Регистрация Спросить otvet5GPT
Еденорожка666
09.05.2023 15:04
Алгебра
Есть ответ 👍

Докажите, что при любом значении b уравнение: (bx^2-x+1)(bx^5-2)=3x^7(b-5) является уравнением седьмой степени;

266
439
Посмотреть ответы 2

Ответы на вопрос:

Санёк1616
Санёк1616
4,5(47 оценок)
(bx^2-x+1)(bx^5-2)=3x^7(b-5)раскрываем скобкиbx^7-2bx^2-bx^6-2x+bx^5-2=3bx^7-15x^7 все с b влево все остальное вправоbx^7-2bx^2-bx^6+bx^5-3bx^7=-15x^7 +2x+2 справа 7 степень независимо от b
juliajulia005
juliajulia005
4,7(43 оценок)

x\in\varnothing

Объяснение:

4x^2-3x+9=0\\D=9-144=-135<0

Значит уравнение не имеет корней.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS