1)выпишите одночлены,получающиеся при умножении одночлена 2x² на каждый из членов многочлена x³-3x+5 2)умножьте многочлен 3a-b на одночлен -2b² 3)решите уравнение 2x(2x-3)+4x(5-x)=0 4)умножьте одночлен -5by² на многочлен 2b²y-b³ 5)умножьте многочлен x²+xy+y² на одночлен 5xy

130

226

Посмотреть ответы 2

Ответы на вопрос:

vikfffff

Алгебра

4,4(36 оценок)

2х²(х³- 3х+5)=2х^5 - 6х³+10х²

одночлены: 2х^5, -6х³, 10х².

(3a - b)*(-2b²)= - 6ab²+2b³

2х(2х-3)+4х(5-х)=0

4х² - 6х+20х - 4х²=0

14х=0

х=0

-5by²(2b²y - b³)= - 10b³y³+5b^(4)y²

(x²+xy+y²)*5xy=5x³y+5x^(4)y²+5xy³

14Dana14

Алгебра

4,6(83 оценок)

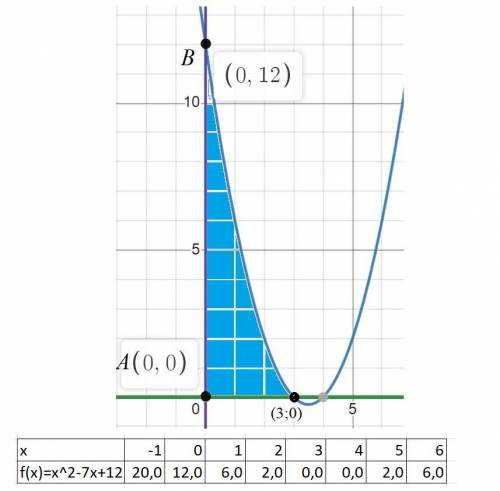
ответ: 13.5 кв.ед.

Объяснение:

Строим графики функций

y=x^2-7x+12; y=0; x=0. (См. скриншот).

Площадь находим по формуле Ньютона-Лейбница

S(ABC) = ∫ₐᵇf(x)dx = F(x)|ₐᵇ = F(b) - F(a).

Пределы интегрирования находим по графику a=0; b=3.

f(x) = x^2-7x+12.

S(ABC) = ∫₀³(x^2-7x+12)dx = ∫₀³ x^2dx - 7∫₀³xdx + 12∫₀³dx = 13.5 кв.ед.

1) ∫₀³ x²dx = x³/3|₀³ = 1/3(3³-0³) = 27/3=9 кв.ед.

2) 7 ∫₀³xdx = 7(x²/2|₀³) = 7/2(3²-0²) = 63/2 = 31.5 кв.ед.

3) 12∫₀³dx = 12 (x|₀³) =12(3-0) = 12*3=36 кв.ед.

S(ABC) = 9-31.5+36 = 13.5 кв.ед.

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.