Алгебра: Найдите область определения функции f(x)=корень 4x^2-1

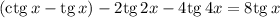
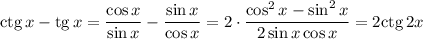
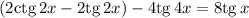
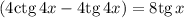
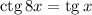
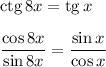
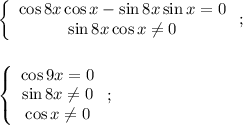
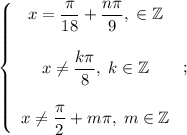
(см. объяснение)Объяснение:Выполним хитрое преобразование:Я не с проста выделил скобками разность тангенса и котангенса.Давайте разберемся в чем здесь секрет:О чудо! Уравнение приняло вид:Думаю теперь не возникает вопросов, что делать.Ведь теперь алгоритм решения стал прозрачным:И снова сжимаем уравнение:Теперь осталось решить то, что записано выше:Тогда:И эту систему можно записать покороче:Уравнение решено!...

debiltrue

20.05.2021 08:41

Алгебра

Есть ответ 👍

Найдите область определения функции f(x)=корень 4x^2-1

116

129

Посмотреть ответы 2

Ответы на вопрос:

slava20syper

Алгебра

4,5(6 оценок)

4x² - 1 ≥ 0

4x² ≥ 1

x₁ = 1/2

x₂ = - 1/2

d(f) = ( -∞; -0,5 ) ∪ ( 0,5; +∞ )

Safaran2003

Алгебра

4,7(82 оценок)

(см. объяснение)

Объяснение:

$\mathrm{ctg}\,x-2\mathrm{tg}\,2x-4\mathrm{tg}\,4x=9\mathrm{tg}\,x$

Выполним "хитрое" преобразование:

$\left(\mathrm{ctg}\,x-\mathrm{tg}\,x\right)-2\mathrm{tg}\,2x-4\mathrm{tg}\,4x=8\mathrm{tg}\,x$

Я не с проста выделил скобками разность тангенса и котангенса.

Давайте разберемся в чем здесь секрет:

$\mathrm{ctg}\,x-\mathrm{tg}\,x=\dfrac{\cos x}{\sin x}-\dfrac{\sin x}{\cos x}=2\cdot\dfrac{\cos^2 x-\sin^2 x}{2\sin x\cos x}=2\mathrm{ctg}\,2x$

О чудо! Уравнение приняло вид:

$\left(2\mathrm{ctg}\,2x-2\mathrm{tg}\,2x\right)-4\mathrm{tg}\,4x=8\mathrm{tg}\,x$

Думаю теперь не возникает вопросов, что делать.

Ведь теперь алгоритм решения стал прозрачным:

$\left(4\mathrm{ctg}\,4x-4\mathrm{tg}\,4x\right)=8\mathrm{tg}\,x$

И снова "сжимаем" уравнение:

$\mathrm{ctg}\,8x=\mathrm{tg}\,x$

Теперь осталось решить то, что записано выше:

$\mathrm{ctg}\,8x=\mathrm{tg}\,xdfrac{\cos 8x}{\sin 8x}=\dfrac{\sin x}{\cos x}\\$

$\left\{\begin{array}{c}\cos 8x\cos x-\sin 8x\sin x=0\\\sin 8x\cos x\ne 0\end{array}\right;left\{\begin{array}{c}\cos 9x=0\\\sin 8x\ne0\\\cos x\ne 0\end{array}\right;$

Тогда:

$\left\{\begin{array}{c}x=\dfrac{\pi}{18}+\dfrac{n\pi}{9},\;\n\in\mathbb{Z}x\ne\dfrac{k\pi}{8},\;k\in\mathbb{Z}x\ne\dfrac{\pi}{2}+m\pi,\;m\in\mathbb{Z}\end{array}\right;$

И эту систему можно записать покороче:

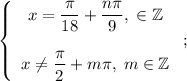
$\left\{\begin{array}{c}x=\dfrac{\pi}{18}+\dfrac{n\pi}{9},\;\n\in\mathbb{Z}x\ne\dfrac{\pi}{2}+m\pi,\;m\in\mathbb{Z}\end{array}\right;$

Уравнение решено!

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.