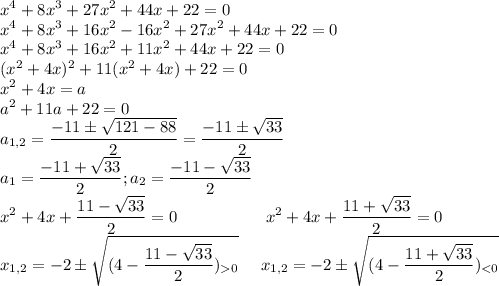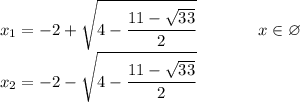Регистрация Спросить otvet5GPT
kaznacheev27p070e2
12.05.2022 08:16
Алгебра
Есть ответ 👍

Докажите, что при любых значениях x и y имеет место неравенство x^2 + 10y^2 - 6xy +10 x - 26 y + 30 > 0

233
299
Посмотреть ответы 2

Ответы на вопрос:

кот7891
кот7891
4,8(4 оценок)

x^2 + 10y^2 - 6xy +10 x - 26 y + 30> 0

перепишем неравенство в виде

x^2 - 2x(3y-5) +(3y-5)^2-(3y-5)^2+ 10y^2 - 26 y + 30> 0

используя формулу квадрата двучлена

(x-3y+5)^2 -9y^2+30y-25+ 10y^2 - 26 y + 30> 0

сводя подобные члены

(x-3y+5)^2 +y^2 +4 y + 5> 0

перепишем в виде

(x-3y+5)^2 +y^2 +4 y + 4+1> 0

группируя

(x-3y+5)^2 +(y^2 +4 y + 4)+1> 0

используя формулу квадрата двучлена

(x-3y+5)^2 +(y +2)^2 +1> 0

 

квадрат любого выражения неотрицателен,

сумма двух неотрицатеьных выражений неотрицательна

сумма неотрицательного выражения и положительного величина положительная

поэтому (x-3y+5)^2 +(y +2)^2 +1> 0 верно для любых значений x и y, а значит

и исходное неравенство x^2 + 10y^2 - 6xy +10 x - 26 y + 30 > 0

доказано

 

ttommy
ttommy
4,6(34 оценок)

\displaystyle x^4+8x^3+27x^2+44x+22=0\\x^4+8x^3+16x^2-16x^2+27x^2+44x+22=0\\x^4+8x^3+16x^2+11x^2+44x+22=0\\(x^2+4x)^2+11(x^2+4x)+22=0\\x^2+4x=a\\a^2+11a+22=0\\a_{1,2}=\frac{-11\pm\sqrt{121-88}}{2}=\frac{-11\pm\sqrt{33}}{2}\\a_1=\frac{-11+\sqrt{33}}{2};a_2=\frac{-11-\sqrt{33}}{2}\\x^2+4x+\frac{11-\sqrt{33}}{2}=0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x^2+4x+\frac{11+\sqrt{33}}{2}=0\\x_{1,2}=-2\pm\sqrt{(4-\frac{11-\sqrt{33}}{2})_{0}}\ \ \ \ x_{1,2}=-2\pm\sqrt{(4-\frac{11+\sqrt{33}}{2})_{

\displaystyle x_1=-2+\sqrt{4-\frac{11-\sqrt{33}}{2}}\ \ \ \ \ \ \ \ \ \ \ x\in\varnothing\\x_2=-2-\sqrt{4-\frac{11-\sqrt{33}}{2}}

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS