Регистрация Спросить otvet5GPT
Avetodor
23.09.2022 10:03
Алгебра
Есть ответ 👍

Нужна по . оцените значение выражения 2m; 2m+3; -m; 1-m, если: 1) 2

106
217
Посмотреть ответы 2

Ответы на вопрос:

vladgas78
vladgas78
4,4(26 оценок)

Д91
Д91
4,7(44 оценок)

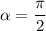
$\alpha = \frac{\pi}{2}$  

та

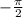
     -\frac{\pi}{2}$

Объяснение:

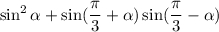
$\sin^2 \alpha + \sin(\frac{\pi}{3}+\alpha) \sin(\frac{\pi}{3}-\alpha)$

$= \sin^2 \alpha + \frac{1}{2}[\cos(\alpha)\sin(\frac{\pi}{3})+\sin(\alpha)\cos(\frac{\pi}{3})][\cos(\alpha)\sin(\frac{\pi}{3})-\sin(\alpha)\cos(\frac{\pi}{3})]$

$= \sin^2 \alpha + \frac{1}{2}[\frac{\sqrt{3}}{2}\cos(\alpha)+\frac{1}{2}\sin(\alpha)][\frac{\sqrt{3}}{2}\cos(\alpha)-\frac{1}{2}\sin(\alpha)]$$= \sin^2 \alpha + \frac{1}{4}[\frac{3}{4}\cos^2(\alpha)-\frac{1}{4}\sin^2(\alpha)]$

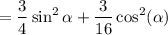
$= \frac{3}{4}\sin^2 \alpha + \frac{3}{16}\cos^2(\alpha)$

Тепер ми можемо записати рівняння у наступному вигляді:

$\frac{3}{4}\sin^2 \alpha + \frac{3}{16}\cos^2(\alpha) = \frac{3}{4}$

Множачею обох частин на $\frac{16}{3}$  ми отримуємо:

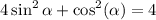
$4\sin^2 \alpha + \cos^2(\alpha) = 4$

Використовуючи тригонометричну тотожність 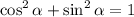$\cos^2 \alpha + \sin^2 \alpha = 1$, ми можемо записати:

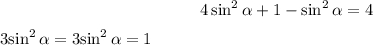
$4\sin^2 \alpha + 1 - \sin^2 \alpha = 4$$3\sin^2 \alpha = 3$$\sin^2 \alpha = 1$

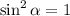Оскільки $\sin^2 \alpha$ не може бути більше 1, ми можемо зробити висновок, що $\sin^2 \alpha = 1$ означає, що 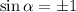$\sin \alpha = \pm 1$. Таким чином, рівняння має два розв'язки: 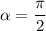$\alpha = \frac{\pi}{2}$ та $\alpha = -\frac{\pi}{2}$.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS