Регистрация Спросить otvet5GPT
VadimRichard
26.08.2022 07:42
Алгебра
Есть ответ 👍

Решить тригонометрическое 2cos x+корень3=0 распишите

136
337
Посмотреть ответы 2

Ответы на вопрос:

Makeev20
Makeev20
4,4(58 оценок)

решение: 2cosx + √3 = 02cosx = - √3cosx = - √3/2x = ± arccos( - √3/2) + 2πn, n ∊ zx = ± (π - arccos√3/2) + 2πn, n ∊ zx = ± ( π - π/6) + 2πn, n ∊ zх = ± 5π/6 + 2πn, n ∊ zответ: = ± 5π/6 + 2πn, n ∊ z.

azovska552
azovska552
4,6(46 оценок)

2n+1

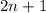
Объяснение:

(1) - отняли n-ую строку от каждой из остальных.

(2) - вычитаем из последней строки все остальные, домноженные на 2

(3) - разложим определитель по элементам n-ой строки

(4) - определитель единичной матрицы порядка n-1 равен 1 ∀n>1, n∈N.

\begin{equation*}\left|\begin{array}{ccccc}3 & 2 & 2 & \ldots & 2\\2 & 3 & 2 & \ldots & 2\\ 2 & 2 & 3 & \ldots & 2\\\vdots & \vdots & \vdots & \ddots & \vdots\\2 & 2 & 2 & \ldots & 3\end{array}\right|\stackrel{=}{(1)}\left|\begin{array}{ccccc}1 & 0 & 0 & \ldots & -1\\0 & 1 & 0 & \ldots & -1\\ 0 & 0 & 1 & \ldots & -1\\\vdots & \vdots & \vdots & \ddots & \vdots\\2 & 2 & 2 & \ldots & 3\end{array}\right|\stackrel{=}{(2)}\end{equation*}

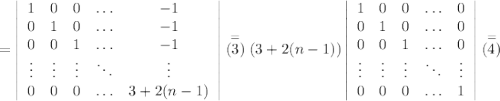
\begin{equation*}=\left|\begin{array}{ccccc}1 & 0 & 0 & \ldots & -1\\0 & 1 & 0 & \ldots & -1\\ 0 & 0 & 1 & \ldots & -1\\\vdots & \vdots & \vdots & \ddots & \vdots\\0 & 0 & 0 & \ldots & 3+2(n-1)\end{array}\right|\stackrel{=}{(3)}(3+2(n-1))\left|\begin{array}{ccccc}1 & 0 & 0 & \ldots & 0\\0 & 1 & 0 & \ldots & 0\\ 0 & 0 & 1 & \ldots & 0\\\vdots & \vdots & \vdots & \ddots & \vdots\\0 & 0 & 0 & \ldots & 1\end{array}\right|\stackrel{=}{(4)}\end{equation*}

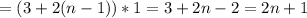
=(3+2(n-1))*1=3+2n-2=2n+1

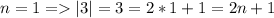
n=1=|3|=3=2*1+1=2n+1

А значит для любого натурального n данный определитель равен 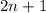2n+1

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS