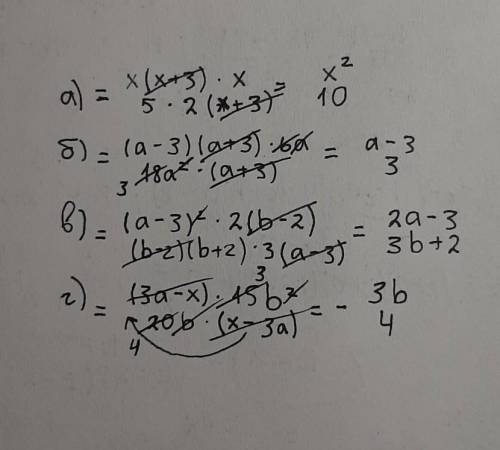квадратичную форму к каноническому виду методом ортогональных преобразований p.s. перепроверял несколько раз получаются нулевые собственные векторы. объясните в чем ошибка

282

302

Посмотреть ответы 2

Ответы на вопрос:

maks197rus

Математика

4,4(58 оценок)

Матрица, соответствующая данной квадратичной форме: нужно найти собственные числа и собственные вектора этой матрицы. собственные числа находим из уравнения det(a - λe) = 0: прибавим к первой строке все остальные строки, после вынесения общего множителя обнулим первый столбик во всех строках, кроме первой: раскладываем определитель по первому столбцу. опустим пока множитель (1 - λ), сложим прибавим к третьей строчке вторую, вынесем общий множитель и обнулим третий столбец везде, кроме последней строки: раскладываем определитель по третьему столбцу, после отбрасывания множителей остается определитель матрицы 2x2, который равен итак, находим собственные векторы: 1) с.ч. = 1 сумма всех строк равна 0, выкинем последнюю. матрицу к красивому виду (насколько сможем): из полученного вида матрицы получаем, что уравнению удовлетворяют все вектора вида (a, a, a, a); с.в. (1, 1, 1, 1) 2) c.ч. = -1 с.в. (1, 1, -1, -1) 3) с.ч. = -3 с.в. (1, -1, -1, 1) 4) с.ч. = 7 c.в. (1, -1, 1, -1) собственные вектора уже ортогональны, но еще не отнормированы. длина каждого равна 1/2, так что окончательно получаем, что под действием замены (по столбцам записаны собственные векторы) квадратичная форма примет вид

PowerSell

Математика

4,6(84 оценок)

Пошаговое объяснение:

решение на фото.......

Решите нужно именно решить!! (не с ф0томес

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.