saneok67p086je

04.09.2022 14:33

Геометрия

Есть ответ 👍

Перепендикуляр, проведённый из середины основы равнобедренного треугольника на боковую сторону, делит её на отрезки длиною 16 см и 11см, считая от угла при вершине треугольника. найдите площадь треугольника.

231

278

Посмотреть ответы 2

Ответы на вопрос:

WooLFooS

Геометрия

4,6(73 оценок)

Ответ: площадь равна 216

tsey12kirill

Геометрия

4,6(46 оценок)

Дано:

Правильная четырёхугольная пирамида.

АВ = 8

∠SCD = 60˚

Найти:

V - ?

Решение:

"Правильный многоугольник - многоугольник. у которого все углы и стороны равны".

Так как у нас данная пирамида - правильная, четырёхугольная => основание этой пирамиды - квадрат.

"Квадрат - геометрическая фигура, у которой все стороны равны".

=> АВ = ВС = AD = CD = 8 см.

S квадрата = а², где а - сторона квадрата.

S квадрата = 8² = 64 см²

Проведём апофему SЕ к стороне CD.

"Апофема - высота боковой грани пирамиды, проведённая к основанию".

"Апофема делит сторону основания на две равные части".

△СSD - равносторонний, так как он находится в правильном многоугольнике.

=> его все углы равны по 60°.

СЕ = ED = 8/2 = 4

△SEC и △SED - прямоугольные, так как SE - высота.

"Если угол прямоугольного треугольника равен 60°, то напротив лежащий катет равен произведению меньшего катета на √3".

=> SE = 4 * √3 = 4√3

h - высота квадрата.

h = AB = BC = CD = AD = 8 см.

Обозначим центр квадрата буквой О.

Обозначим на середину АВ точкой F.

=> ЕО = FO = 8/2 = 4 см.

Найдём высоту пирамиды SO, по теореме Пифагора: (с = √(a² + b²), где с - гипотенуза; а, b - катеты)

а = √(c² - b²) = √((4√3)² - 4²) = √(16 - (3 - 1)) = √32 = 4√2

Итак, SO = 4√2

V = 1/3S квадрата * SO = 1/3 * 64 * 4√2 = 256√(2)/3 ед.куб.

ответ: 256√(2)/3 ед.куб.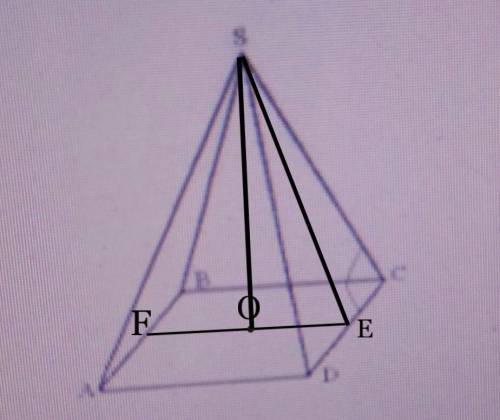
В правильной четырехугольной пирамиде со стороной основания 8 и углом между стороной основания и бок

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.