Водный раствор содержал 140 г воды. через некоторое время 50 г воды испарили, после чего концентрация соли увеличилась на 10%. сколько граммов соли содержит раствор? решить,

180

257

Посмотреть ответы 2

Ответы на вопрос:

Лолик1112

Алгебра

4,5(6 оценок)

Решение: обозначим количество соли в растворе за (х) г, тогда первоначальный вес раствора составлял: (х+140) г, а концентрация соли в растворе составляла: х/(х+140)*100% после испарения воды на 50г, содержание воды в растворе стало равным: 140-50=90 (г), а вес раствора после испарения воды равен: (х+90) г концентрация получившегося раствора составила: х/(х+90)*100% а так как концентрация получившегося раствора на 10% больше первоначального раствора, составим уравнение: х/(х+90)*100% - х/(х+140)*100%=10% разделим на 10: х/(х+90)*10 - х/(х+140)*10)=1 10*(х+140)*х - 10*(х+90)*х=1*(х+140)*(х+90) 10х²+1400х - 10х²-900х=х²+140х+90х+12600 500х=х²+230х+12600 х²+230х+12600-500х=0 х²-270х+12600=0 х1,2=(270+-d)*2*1 d=√(72900-4*1*12600)=√(72900-50400)=√22500=150 х1,2=(270+-150)/2 х1=(270+150)/2 х1=420/2 х1=210 - не соответствует условию , т.к количество соли превысило бы количество воды х2=(270-150)/2 х2=120/2 х2=60 (грамм- это количество соли содержалось в растворе) ответ: содержание соли в растворе 60г

kristos24052006

Алгебра

4,5(23 оценок)

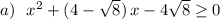
$a)\ \ x^2+(4-\sqrt8)\, x-4\sqrt8\geq 0$

Нули функции можно легко найти по теореме Виета.

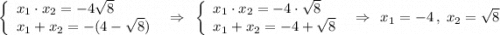
$\left\{\begin{array}{l}x_1\cdot x_2=-4\sqrt8\\x_1+x_2=-(4-\sqrt8)\end{array}\right\ \ \Rightarrow \ \ \left\{\begin{array}{l}x_1\cdot x_2=-4\cdot \sqrt8\\x_1+x_2=-4+\sqrt8\end{array}\right\ \ \Rightarrow \ \ x_1=-4\ ,\ x_2=\sqrt8$

Отметим нули функции на числовой оси и вычислим знаки в образовавшихся промежутках .

$+++[-4\, ]---[\, \sqrt8\, ]+++$

Выбираем промежутки, где стоят знаки плюс .

$x\in (-\infty \, ;-4\ ]\cup [\ \sqrt8\ ;+\infty \, )\ \ \Rightarrow \ \ x\in (-\infty \, ;-4\ ]\cup [\ 2\sqrt2\ ;+\infty \, )$

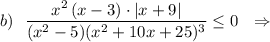
$b)\ \ \dfrac{x^2\, (x-3)\cdot |x+9|}{(x^2-5)(x^2+10x+25)^3}\leq 0\ \ \Rightarrow$

Разложим на множители знаменатель.

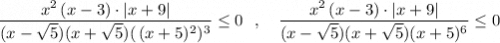
$\dfrac{x^2\, (x-3)\cdot |x+9|}{(x-\sqrt5)(x+\sqrt5)\cdor (\, (x+5)^2)^3}\leq 0\ \ ,\ \ \ \dfrac{x^2\, (x-3)\cdot |x+9|}{(x-\sqrt5)(x+\sqrt5)\cdor (x+5)^6}\leq 0$

Нули числителя: 0 , 3 , -9 .

Нули знаменателя: 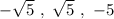$-\sqrt5\ ,\ \sqrt5\ ,\ -5$ . При этих значениях переменной точки на оси выколем, т.к. знаменатель не может равняться 0 .

$---[-9]---(-5)---(-\sqrt5)+++[\ 0\ ]+++(\sqrt5)---[\ 3\ ]+++$

Выбираем знаки минус и точки, где дробь может быть равна 0 .

$x\in (-\infty ;-5\, )\cup (-5\, ;-\sqrt5\, )\cup \{\ 0\ \}\cup (\, \sqrt5\, ;\ 3\ ]$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.