Регистрация Спросить otvet5GPT
anelya1429
21.01.2022 16:14
Математика
Есть ответ 👍

Как найти объём если грань равна 49см квадратных

155
267
Посмотреть ответы 2

Ответы на вопрос:

larisa115
larisa115
4,7(70 оценок)
  предположим , что надо найти объём куба. а= корень квадратный из 49=7 см v=9*9*9=729 (см3)
abcdefgh
abcdefgh
4,7(38 оценок)
Дано:

△ABC - равнобедренный;

P△ABC = 36, AB = 16.

Найти:

S△ABC = ? (ед. кв).

Решение:

Т.к. △ABC - равнобедренный ⇒ AC = CB, по свойству равнобедренного тр-ка.

Предположим, что основание составляет 16. Тогда:

AC = CB = (36 - 16) : 2 = 20 : 2 = 10.

Проверим, верно ли это по теореме о неравенстве тр-ка.

"Каждая сторона треугольника меньше суммы двух других сторон".

⇒ 16 + 10 > 10, 10 + 10 > 16, 10 + 16 > 16 (всё совпадает, поэтому боковую сторону и основание мы нашли верно).

Формула площади треугольника выглядит следующим образом:

S△ = 1/2 ⋅ a ⋅ h, где a - основание (AB), h - высота.

Проведём из точки B к основанию равнобедренного тр-ка высоту CH. При этом у нас образовалось два равных прямоугольных треугольника ACH и BCH (их равенство можно доказать по всем признакам равенства прямоугольных тр-ков, исходя из того, что △ABC - равнобедренный).

"В равнобедренном треугольнике высота, проведённая к основанию, является медианой и биссектрисой".

⇒ CH является медианой и делит основание AB так, что AH = HB = 16 : 2 = 8.

Найдём высоту равнобедренного тр-ка ABC по теореме Пифагора (a = √(c² - b²), где a и b - катеты, c - гипотенуза).

CH = √(AC² - AH²) = √(10² - 8²) = √(100 - 64) = √36 = 6.

CH = √(CB² - HB²) = √(10² - 8²) = √(100 - 64) = √36 = 6.

Найдём площадь равнобедренного тр-ка ABC по указанной выше формуле:

S△ABC = 1/2 ⋅ 16 ⋅ 6 = 16/2 ⋅ 6 = 8 ⋅ 6 = 48 (ед. кв).

ответ: 48 (ед. кв).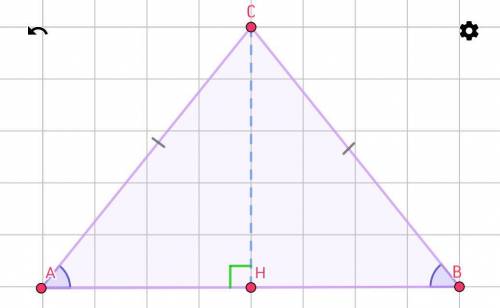
ABC-равнобедренний треугольникP=36AB=16Ниайдите Площадь

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS