Две пятых умножить на шесть девятых, одна целя одна четвертая умножить на две целых две тритих,три целых одна третья умножить на она целая одна пятая,пять целых одна вторая умножить на две целых две одиннадцатых
218
413
Ответы на вопрос:
1.
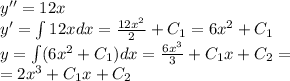
общее решение
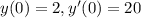
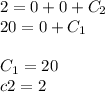
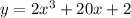
частное решение
2.
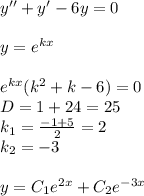
общее решение
3.
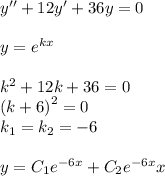
общее решение
4.
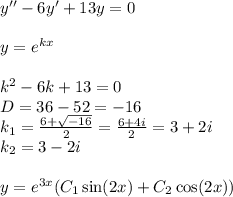
общее решение
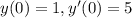
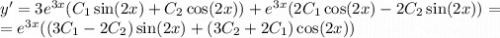
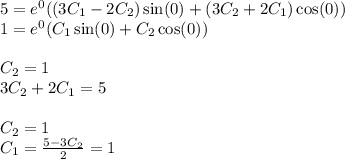
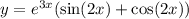
частное решение
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Решите . в рукописи 80 стр. за день машинистка перепечатала 4\5...
 katerinabuzmk03.01.2022 06:33
katerinabuzmk03.01.2022 06:33 -
Как эти решение ? 6318х25+3682х25 4000х26+5000х26...
 alex2002fedorov25.01.2021 08:11
alex2002fedorov25.01.2021 08:11 -
Из куска ткани можно сшить 12 детских плащей, расходуя на каждый...
 manovskidominik04.04.2020 13:05
manovskidominik04.04.2020 13:05 -
Средняя арифметическая скоростей по течению против течения лодки...
 archakova6518.02.2023 04:49
archakova6518.02.2023 04:49 -
Выполните в столбик деление с остатком примеры 209: 29 212: 56 1550:...
 Корни25.07.2020 15:51
Корни25.07.2020 15:51 -
Обчислити суми трьома за зразком 32+55...
 Дэникс102.05.2022 09:06
Дэникс102.05.2022 09:06 -
(807*23-73 во второй степени -416: 13): 16 как решить...
 Dikaya2410.03.2023 13:45
Dikaya2410.03.2023 13:45 -
(3х+1)² + (4х-3)(4х+3) = 5х(5х-2) решите уравнение с формул сокращённого...
 лобарант16.04.2022 13:10
лобарант16.04.2022 13:10 -
Раскройте скобки в выражении и его (a-8,4)+(3 2/5-a)= (16 5/9- 1/3-b)...
 Ульяна333014.05.2021 02:40
Ульяна333014.05.2021 02:40 -
Чему учила сына мать провожая васютку в тайгу...
 Аля4Б02.05.2023 11:55
Аля4Б02.05.2023 11:55

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
