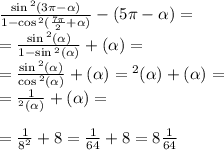Регистрация Спросить otvet5GPT
Kasha26336
10.05.2021 10:38
Алгебра
Есть ответ 👍

Постройте в одной координатной плоскости графики следующих функций: y=, y=, y=, y=. ,тему не понял абсолютно.

275
285
Посмотреть ответы 2

Ответы на вопрос:

Усварппоры
Усварппоры
4,8(99 оценок)
График функции (гр.ф. далее) у=х^2 выглядит как парабола, ветви которой направлены вверх, начало в точке (0; 0), ветви пересекают точки (-1: 1) и (1; 1) соответственно.  гр.ф у=х^2-2 выглядит ровно так же, как и предыдущий, но опущенный на две клетки вниз, т.е. начало в точке (0; -2), ветви проходят ччерез точки (-1; -2) и (1; -2). гр.ф. у=1,5х^2 такой же, как и первый график, все точки те же, но дальше ветви будут у'же (чуть ближе располагаться к оси оу), чем первый график. гр.ф. у=-х^2 +3 такой же, как и второй, но не опущенный на две, а поднятый на три клетки вверх и ветви у него будут направлены вниз (при этом ветви всех предыдущих вверх направлены). т.е. начало в точке (0; 3), ветви пересекают точки (-1; 2) и (1; 2). гр.ф. у= (х +2)^2 выглядит как парабола, ветви которой направлены вверх. такая же, как и первая, но сдвинутая на две клетки влево. т.е. начало в точке (-2; 0), ветви проходят через точки (-3; 0) и (-1; 0).
Pussyellien
Pussyellien
4,4(61 оценок)

\frac{ \sin {}^{2} (3\pi - \alpha ) }{1 - \cos {}^{2} ( \frac{7\pi}{2} + \alpha ) } - \ctg(5\pi - \alpha ) = \\ = \frac{ \sin {}^{2} ( \alpha ) }{1 - \sin {}^{2} ( \alpha ) } + \ctg( \alpha ) = \\ = \frac{ \sin {}^{2} ( \alpha ) }{ \cos {}^{2} ( \alpha ) } + \ctg( \alpha ) = \tg {}^{2} ( \alpha ) + \ctg( \alpha ) = \\ = \frac{1}{\ctg {}^{2} (\alpha )} + \ctg (\alpha) = \\ \\ = \frac{1}{ {8}^{2} } + 8 = \frac{1}{64} + 8 = 8 \frac{1}{64}

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS