Регистрация Спросить otvet5GPT
арина1198
28.03.2022 03:34
Математика
Есть ответ 👍

Найти первообразную для функции в точке: 1)f(x)=15x^4 (1; 0) 2)f(x)=20x (4; 5) 3)f(x)=12x^5 (0; 1)

244
434
Посмотреть ответы 2

Ответы на вопрос:

ablyaev98
ablyaev98
4,6(47 оценок)
1)f(x)=15x^4 f(x) =3x^5+c f(1)=0 3*1^5+c=0 c=-3 f(x)=3x^5-3 2)f(x)=20x f(x) =10x^2+c f(4)=5 10*4^2+c=5 160+c=5 c=-155 f(x)=10x^2-155 3) f(x)=12x^5 f(x) =2x^6+c f(0)=1 2*0^6+c=1 c=1 f(x)=2x^2+1
просмь
просмь
4,6(79 оценок)
Решение:

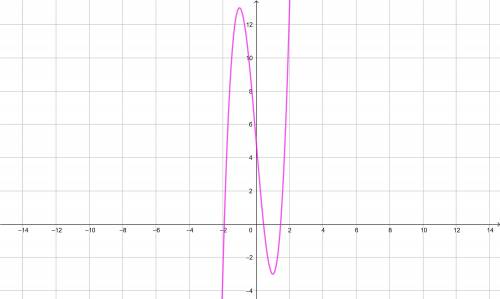
Для начала найдём производную данной функции:

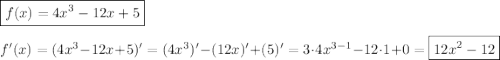
\boxed{f(x)=4{x}^{3}-12x+5} \\ \\ f'(x)=(4{x}^{3}-12x+5)'=(4{x}^{3})'-(12x)'+(5)'=3\cdot4{x}^{3-1}-12\cdot1+0=\boxed{12x^2-12}

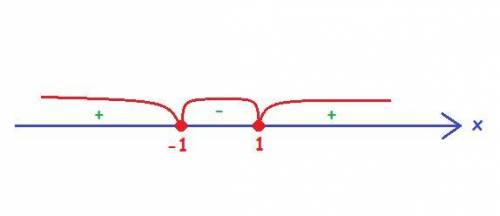
Теперь найдём критические точки, приравнивая производную к нулю:

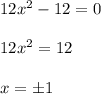
12{x}^{2}-12=0 \\ \\ 12x^2=12 \\ \\ x=\pm 1

Итак критические точки: 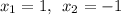x_1=1, \: \: x_2=-1.

Устанавливаем знак производной на каждом интервале (см рисунок).

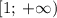Функция возрастает на каждом из промежутков (-\infty; \: -1] и [1; \: +\infty).

То есть функция убывает на промежутке \boxed{[-1; \: 1]}.

ответ: \Large{\boxed{[-1; \: 1]}}
Найдите промежуток убывания функции > f(x)=4х^3-12х+5полное решение!
Найдите промежуток убывания функции > f(x)=4х^3-12х+5полное решение!

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS