При каких значениях b уравнение x^2 + bx + 3b=0 имеет единственное решение?

224

429

Посмотреть ответы 3

Ответы на вопрос:

Crackstack18

Алгебра

4,6(4 оценок)

X^2+bx+3b=0 a=1, b=b, c=3b. d=b^2-4*a*c d=b^2-12b. квадратное уравнение имеет 1 корень, когда дискриминант равен 0. отсюда: b^2-12b=0 b*(b-12)=0 b1=0 b2=12 таким образом, при b=0 и 12 данное уравнение имеет один корень. ответ: 0 и 12.

Enot811

Алгебра

4,4(87 оценок)

X² + bx + 3b = 0 d = b² - 4ac = b² - 12b уравнение имеет 1 корень, если ответ: при b = 0 и при b = 12

irinalove2

Алгебра

4,8(39 оценок)

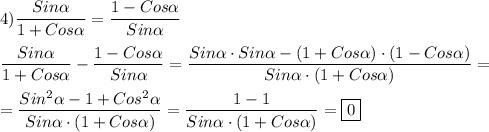
$4)\dfrac{Sin\alpha}{1+Cos\alpha } =\dfrac{1-Cos\alpha }{Sin\alpha}dfrac{Sin\alpha}{1+Cos\alpha } -\dfrac{1-Cos\alpha }{Sin\alpha }=\dfrac{Sin\alpha\cdot Sin\alpha-(1+Cos\alpha)\cdot(1-Cos\alpha)}{Sin\alpha\cdot(1+Cos\alpha)} ==\dfrac{Sin^{2}\alpha-1+Cos^{2}\alpha}{Sin\alpha\cdot(1+Cos\alpha)}=\dfrac{1-1}{Sin\alpha\cdot(1+Cos\alpha)}=\boxed0$

Если разность левой и провой частей тождества равна нулю, то они равны . Тождество доказано .

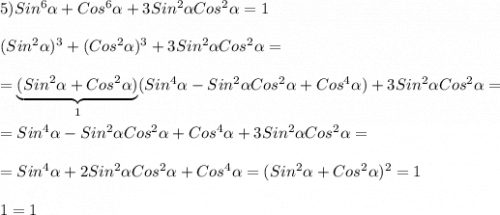
$5)Sin^{6}\alpha +Cos^{6}\alpha+3Sin^{2}\alpha Cos^{2}\alpha=1(Sin^{2}\alpha )^{3}+(Cos^{2}\alpha )^{3}+3Sin^{2}\alpha Cos^{2}\alpha==\underbrace{(Sin^{2}\alpha +Cos^{2}\alpha)}_{1}(Sin^{4} \alpha-Sin^{2}\alpha Cos^{2}\alpha +Cos^{4}\alpha)+3Sin^{2}\alpha Cos^{2}\alpha==Sin^{4} \alpha-Sin^{2}\alpha Cos^{2}\alpha +Cos^{4}\alpha+3Sin^{2}\alpha Cos^{2}\alpha==Sin^{4} \alpha+2Sin^{2}\alpha Cos^{2}\alpha +Cos^{4}\alpha=(Sin^{2}\alpha+Cos^{2}\alpha)^{2}=11=1$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.