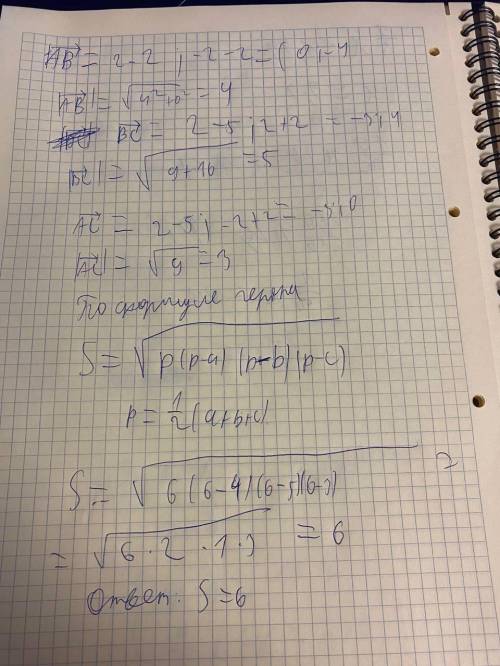Решение по ! ! 4. две окружности с радиусами 4 см и 6 см касаются снаружи. их общая касательная, которая не проходит через точку соприкосновения кругов, пересекает линию центров в точке а. найдите расстояния от точки а в центры кругов.

135

470

Посмотреть ответы 2

Ответы на вопрос:

Maowsk

Геометрия

4,6(56 оценок)

асательная прямая t к окружности c пересекает окружность в единственной точке t. для сравнения, секущие прямые пересекают окружность в двух точках, в то время как некоторые прямые могут не пересекать окружность совсем. это свойство касательной прямой сохраняется при многих преобразованиях[en], таких как подобие, вращение, параллельный перенос, инверсия и картографическая проекция. говоря техническим языком, эти преобразования не меняют структуру инцидентности касательных прямых и окружностей, даже если сами прямые и окружности деформируются.

радиус окружности, проведённый через точку касания, перпендикулярен касательной прямой. и обратно, перпендикуляр к радиусу в конечной точке (на окружности) является касательной прямой. окружность вместе с касательной прямой имеют осевую симметрию относительно радиуса (к точке касания).

по теореме о степени точкипроизведение длин pm•pn для любого луча pmn равно квадрату pt, длине отрезка от точки p до точки касания (отрезок показан красным цветом).

никакая касательная прямая не может проходить через точку внутри окружности, поскольку любая такая прямая должна быть секущей. в то же время для любой точки, лежащей вне круга, можно построить две проходящие через неё касательные прямые. фигура, состоящая из окружности и двух касательных прямых, также обладает осевой симметрией относительно прямой, соединяющей точку p с центром окружности o (см. рисунок справа). в этом случае отрезки от точки p до двух точек касания имеют одинаковую длину. по теореме о степени точки квадрат длины отрезка до точки касания равен степени точки p относительно окружности c. эта степень равна произведению расстояний от точки p до двух точек пересечения окружности любой секущей линией, проходящей через p.

угол θ между хордой и касательной равен половине дуги, заключённой между концами хорды.

касательная прямая t и точка касания t свойством сопряжённости друг другу; это соответствие можно обобщить в идею о полюсе и поляре. такая же взаимосвязь существует между точкой p вне окружности и секущей линией, соединяющей две точки касания.

если точка p лежит вне окружности с центром o, и если касательные прямые из p касаются окружности в точках t и s, то углы ∠tps и ∠tos в сумме 180°.

если хорда tm проведена из точки касания t прямой p t и ∠ptm ≤ 90°, то ∠ptm = (1/2)∠mot.

марго1002

Геометрия

4,5(8 оценок)

S=6 решение ниже , использовал формулу герона

Вершини трикутника знаходяться в точках А((2:-2) В(2;2) і С(5;-2). Знайдіть периметр трикутника

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.