Алгебра: Представьте в виде многочлена 2x(x^4-5x^3+3)

VladOZmsl

09.03.2020 00:39

Алгебра

Есть ответ 👍

Представьте в виде многочлена 2x(x^4-5x^3+3)

186

251

Посмотреть ответы 2

Ответы на вопрос:

поварешка1

Алгебра

4,8(95 оценок)

(3-5х)(1-2х+3х^2)=3-6х+9х^2-5х+10х^2-15х^3=3-11х+19х^2-15х^2

zziimmbboo

Алгебра

4,8(88 оценок)

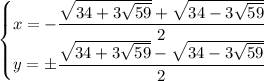
$\begin{cases}x=-\dfrac{\sqrt{34+3\sqrt{59}}+\sqrt{34-3\sqrt{59}}}{2}\\y=\pm\dfrac{\sqrt{34+3\sqrt{59}}-\sqrt{34-3\sqrt{59}}}{2}\end{cases}$

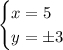
$\begin{cases}x=5\\y=\pm3\end{cases}$

Объяснение:

Чтобы уравнение было менее страшным, введём новые обозначения.

Обозначим x + y = u.

Чтобы было проще извлечь корень

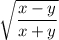
$\sqrt{\dfrac{x-y}{x+y}}$

удобно обозначить x - y = uv², причем для определённости примем v ≥ 0. Тогда весь корень равен просто v.

Решение первого уравнения.

Рассмотрим, что получится, если подставить новые переменные в первое уравнение:

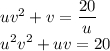
$uv^2+v=\dfrac{20}{u}\\u^2v^2+uv=20$

После замены переменных t = uv получается квадратное уравнение t² + t = 20, корни которого угадываются по теореме Виета, это t = -5 или t = 4.

Итак, uv = -5 или uv = 4. Тогда x - y = uv · v = -5v или 4v.

Первый случай. x - y = -5v

Поскольку по договоренности v ≥ 0, u должно быть отрицательным.

Заметим, что (x - y)² + (x + y)² = x² - 2xy + y² + x² + 2xy + y² = 2(x² + y²) = 68 в соответствии со вторым уравнением. Тогда, подставив новые переменные, получаем:

u² + 25v² = 68

При этом u² · 25v² = 25(uv)² = 25², значит по теореме Виета u² и 25v² — корни квадратного уравнения t² - 68t + 25² = 0.

Выделяем полный квадрат: t² - 68t + 25² = t² - 2 · 34t + 34² + (25² - 34²) = (t - 34)² + (25 - 34)(25 + 34) = (t - 34)² - 9 · 59

Значит, t = 34 ± 3√59 — оба корня положительные. Получаем два варианта:

1) 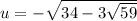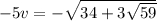$u=-\sqrt{34-3\sqrt{59}}$ , $-5v=-\sqrt{34+3\sqrt{59}}$ . В терминах x и y это приводит к такой системе уравнений:

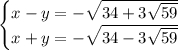
$\begin{cases}x-y=-\sqrt{34+3\sqrt{59}}\\x+y=-\sqrt{34-3\sqrt{59}}\end{cases}$

Полусумма и полуразность этих уравнений даёт x и y

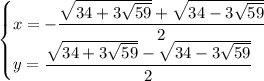
$\begin{cases}x=-\dfrac{\sqrt{34+3\sqrt{59}}+\sqrt{34-3\sqrt{59}}}{2}\\y=\dfrac{\sqrt{34+3\sqrt{59}}-\sqrt{34-3\sqrt{59}}}{2}\end{cases}$

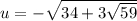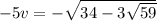2) $u=-\sqrt{34+3\sqrt{59}}$ , $-5v=-\sqrt{34-3\sqrt{59}}$ . Аналогично,

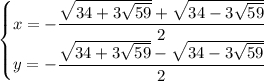
$\begin{cases}x=-\dfrac{\sqrt{34+3\sqrt{59}}+\sqrt{34-3\sqrt{59}}}{2}\\y=-\dfrac{\sqrt{34+3\sqrt{59}}-\sqrt{34-3\sqrt{59}}}{2}\end{cases}$

Второй случай. x - y = 4v

Здесь u должно быть положительным. Следуя первому случаю, последовательно находим:

u² + 16v² = 68

При этом u² · 16v² = 16(uv)² = 16², значит по теореме Виета u² и 16v² — корни квадратного уравнения t² - 68t + 16² = 0.

Выделяем полный квадрат: t² - 68t + 16² = t² - 2 · 34t + 34² + (16² - 34²) = (t - 34)² + (16 - 34)(16 + 34) = (t - 34)² - 30²

Значит, t = 34 ± 30, t = 4 или t = 64. Получаем два варианта:

1) u = 2, 4v = 8. В терминах x и y это приводит к такой системе уравнений:

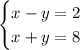
$\begin{cases}x-y=2\\x+y=8\end{cases}$

Решение этой системы уравнений — x = 5, y = 3

2) u = 8, 4v = 2. Аналогично, x = 5, y = -3.

Постскриптум

Решения для "первого случая" (когда x - y = -5v) выглядят громоздко. В принципе, их можно оставить и так, но можно немного упростить.

Попробуем извлечь корень, возможно это как-то . Положим

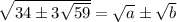
$\sqrt{34\pm3\sqrt{59}}=\sqrt{a}\pm\sqrt{b}$

Возведём в квадрат:

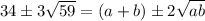
$34\pm3\sqrt{59}=(a+b)\pm2\sqrt{ab}$

Чтобы равенство выполнялось, достаточно потребовать

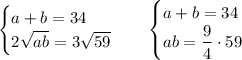
$\begin{cases}a+b=34\\2\sqrt{ab}=3\sqrt{59}\end{cases}\quad\begin{cases}a+b=34\\ab=\dfrac94\cdot{59}\end{cases}$

Еще раз вспоминаем теорему Виета, a и b оказываются корнями уравнения

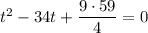
$t^2-34t+\dfrac{9\cdot59}4=0$

Корни этого уравнения 9/2 и 59/2. Так как 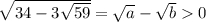$\sqrt{34-3\sqrt{59}}=\sqrt{a}-\sqrt{b} 0$ , то a должно быть больше b. Значит,

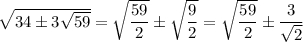
$\sqrt{34\pm3\sqrt{59}}=\sqrt{\dfrac{59}2}\pm\sqrt{\dfrac{9}2}=\sqrt{\dfrac{59}2}\pm\dfrac3{\sqrt{2}}$

Если подставить полученные значения вместо корней в решение для первого случая, получится пара корней

$\left(-\sqrt{\dfrac{59}2},\pm\dfrac3{\sqrt2}\right)$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.