Дядя тофик покупает 9 за 1 манат, а продаёт 3 за 1 манат. какую сумму выручит дядя тофик от продожи 900 ?
260
448
Ответы на вопрос:
(Метод Лагранжа).
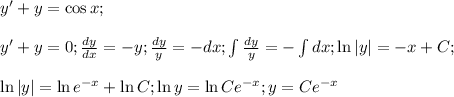
Произвольную постоянную примем за функцию от  .
.
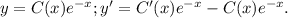
Подставим 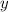 и
и 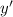 в исходное уравнение:
в исходное уравнение:
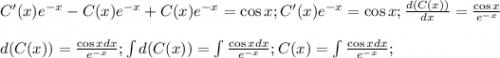
Отдельно найдем полученный неопределенный интеграл:
![\int\frac{\cos{x}dx}{e^{-x}}=\int{e^x\cos{x}}dx;int{e^x\cos{x}}dx=\left[u=e^x; du=e^xdx\atop dv=\cos{x}dx;v=\sin{x}\right]=e^x\sin{x}-\int{e^x\sin{x}dx.}int{e^x\sin{x}dx=\left[u=e^x; du=e^xdx\atop dv=\sin{x}dx;v=-\cos{x}\right]=-e^x\cos{x}+\int{e^x\cos{x}}dx.](/tpl/images/4806/5534/da0d3.png)
Отсюда получаем что:
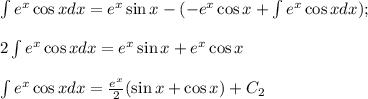
Отсюда получаем что:
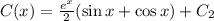
Теперь подставим в формулу 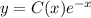 :
:
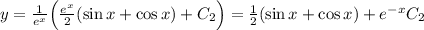
В итоге окончательно получаем:
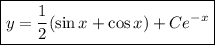
(Метод Бернулли)
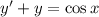
Пусть 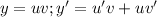 тогда:
тогда:
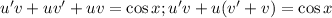 потребуем, чтобы
потребуем, чтобы 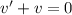 тогда:
тогда:
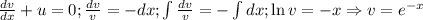
Подставим найденное значение  в
в 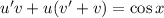 :
:
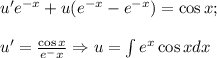
В предыдущем данный интеграл был найден методом интегрирования по частям, поэтому не будет здесь его искать а просто подставим уже найденный.
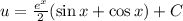 но
но 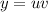 тогда:
тогда:
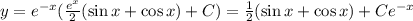 Отсюда получаем:
Отсюда получаем:
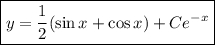
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Написать сочинение про кого нибудь из персонажей кожожаш...
 nastyabro12327.02.2022 05:22
nastyabro12327.02.2022 05:22 -
Выполните вычетания 1/2-(+4) - 5//1)...
 Кузнечик070521.03.2021 16:14
Кузнечик070521.03.2021 16:14 -
2мальчика собрали в саду 64 яблока,сторожь увидел и попросил вернуть,1...
 ponomarevaaaaaaaaaa26.02.2022 06:00
ponomarevaaaaaaaaaa26.02.2022 06:00 -
Уважаемые знатоки, как посчитать какие числа оканчивающиеся на 9 в сумме...
 алекс85821.10.2020 08:01
алекс85821.10.2020 08:01 -
150+150+280+150+1000+ 123+700+911+560+347+ 492=...
 Artur6808405.10.2020 18:22
Artur6808405.10.2020 18:22 -
Первое число состоит из троек (), второе число состоит из того же количества...
 vicky0318.09.2021 13:02
vicky0318.09.2021 13:02 -
Решите . в школьном саду 40 фруктовых деревьев,30 % этих деревьев -яблони.сколько...
 fkbithxtvg21.05.2020 11:15
fkbithxtvg21.05.2020 11:15 -
Реши уравнения x×36=4968×7 920÷x=1 x÷74=132 340-x=0...
 Shamаn1424.02.2023 16:55
Shamаn1424.02.2023 16:55 -
Сколько мальчиков в классе если всего 30 учеников а девочек на 2 больше...
 аян4524.05.2021 02:56
аян4524.05.2021 02:56 -
Особенности адаптационного периода в жизни животного...
 SchoolZnatok09.06.2020 09:07
SchoolZnatok09.06.2020 09:07

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
