Регистрация Спросить otvet5GPT
svetlanakomarova2
06.05.2022 14:15
Алгебра
Есть ответ 👍

Укажите координаты точки а¹ симметричной точке а относительно оси ординат а. а¹(4: 1) б. а¹(4: -1) в. а¹(-4: 1) г. а¹(-4: -1)

197
319
Посмотреть ответы 2

Ответы на вопрос:

frost79naumenkow6nt4
frost79naumenkow6nt4
4,4(96 оценок)
Ответ а(4:
stepanoganezov
stepanoganezov
4,4(92 оценок)

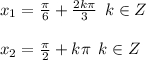
x_{1} = \frac{\pi}{6} + \frac {2k\pi}{3} \: \: k \in Z \\ \\ x_{2} = \frac{\pi}{2} + k\pi \: \: k \in Z

Объяснение:

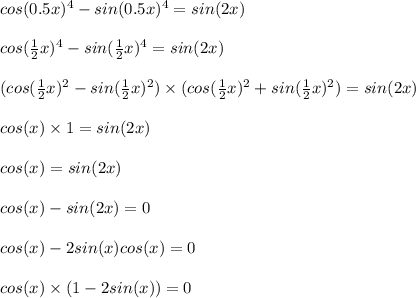
cos(0.5x)^{4} - sin(0.5x)^{4} = sin(2x) \\ \\ cos( \frac{1}{2} x)^{4} - sin( \frac{1}{2} x)^{4} = sin(2x) \\ \\ (cos( \frac{1}{2} x)^{2} - sin( \frac{1}{2} x)^{2} ) \times (cos( \frac{1}{2} x)^{2} + sin( \frac{1}{2} x)^{2} ) = sin(2x) \\ \\ cos(x) \times 1 = sin(2x) \\ \\ cos(x) = sin(2x) \\ \\ cos(x) - sin(2x) = 0 \\ \\ cos(x) - 2sin(x)cos(x) = 0 \\ \\ cos(x) \times (1 - 2sin(x)) = 0

Тогда имеем 2 уравнения —

cos(x) = 01 - 2sin(x) = 0

Решаем —

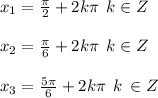
x_{1} = \frac{\pi}{2} + 2k\pi \: \: k \in Z \\ \\ x_{2} = \frac{\pi}{6} + 2k\pi \: \: k \in Z \\ \\ x_{3} = \frac{5\pi}{6} + 2k\pi \: \: k \: \in Z

Находим объединение —

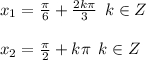
x_{1} = \frac{\pi}{6} + \frac {2k\pi}{3} \: \: k \in Z \\ \\ x_{2} = \frac{\pi}{2} + k\pi \: \: k \in Z

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS