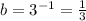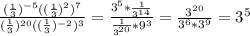Докажите,что квадрат натурального числа на единицу больше произведения двух соседних чисел.

293

381

Посмотреть ответы 2

Ответы на вопрос:

kabdollaevaalia

Математика

4,5(81 оценок)

Пусть некоторое натуральное число равно - n тогда соседние с ним - (n-1) и (n+1) произведение соседних чисел равно (n-1)*(n+1) = n² - 1, что всегда на 1 меньше, чем квадрат среднего - n² - что и требовалось доказать - чтд.

Kristina122205

Математика

4,6(45 оценок)

Пошаговое объяснение:

$b = 3 ^ {-1} = \frac{1}{3}$

$\frac{(\frac{1}{3}) ^ {-5}((\frac{1}{3}) ^ 2) ^ 7}{(\frac{1}{3}) ^ {20}((\frac{1}{3}) ^ {-2}) ^ 3} = \frac{3 ^ 5 * \frac{1}{3 ^ {14}} }{\frac{1}{3 ^ {20}} * 9 ^ 3} = \frac{3 ^ {20}}{3 ^ 6 * 3 ^ 9} = 3 ^ {5}$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.