Регистрация Спросить otvet5GPT
милка327
08.01.2023 23:48
Математика
Есть ответ 👍

Найдите частное решение дифференциального уравнения первого порядка при заданных начальных условиях (х^2+1)у'+4ху=3 у(0)=0

195
305
Посмотреть ответы 1

Ответы на вопрос:

timca2014
timca2014
4,5(28 оценок)

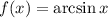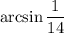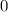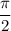Поскольку множеством значений функции f(x)=\arcsin x является отрезок \bigg[{-\dfrac{\pi}{2}};\;\dfrac{\pi}{2}\bigg], то угол  \arcsin\dfrac{1}{14} будет лежать в первом квадранте (от 0 до \dfrac{\pi}{2}).

Соответственно, угол 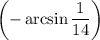\bigg({-\arcsin\dfrac{1}{14}}\bigg) будет лежать в четвертом квадранте (от {-\dfrac{\pi}{2}} до 0).

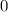Отсюда, прибавив к этому углу 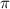\pi, окажемся во втором квадранте (от 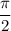\dfrac{\pi}{2} до

Таким образом, искомый угол равен 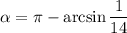\alpha=\pi-\arcsin\dfrac{1}{14}.

Тогда,

\begin{aligned}\mathop{\mathrm{tg}}\alpha&=\mathop{\mathrm{tg}}\bigg(\pi-\arcsin\dfrac{1}{14}\bigg)=-\mathop{\mathrm{tg}}\bigg(\arcsin\dfrac{1}{14}\bigg)=-\dfrac{\sin\arcsin\tfrac{1}{14}}{\cos\arcsin\tfrac{1}{14}}=\\&=-\dfrac{\tfrac{1}{14}}{\sqrt{1-\sin^2\Big(\arcsin\tfrac{1}{14}\Big)}}=-\dfrac{1}{14\cdot\sqrt{1-\tfrac{1}{14^2}}}=-\dfrac{1}{\sqrt{14^2-1}}=\\&=-\dfrac{1}{\sqrt{195}}\end{aligned}

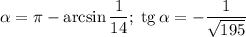
ответ. \alpha=\pi-\arcsin\dfrac{1}{14};\;\mathop{\mathrm{tg}}\alpha=-\dfrac{1}{\sqrt{195}}

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS