Вравнобедренном треугольнике abc ab=bc=13 ac=10 найти расстояние от вершины b до а) точки m пересечения медиан б) точки о1 пересечения биссектрис в) точки о пересечения серединных перпендикуляров сторон г) точки h пересечения высот

250

415

Посмотреть ответы 3

Ответы на вопрос:

софия731

Математика

4,4(4 оценок)

Высоту bh найдём из прямоугольного треугольника bhc, где hc = 5 (1/2 ac), а bc по условию = 13. bh^2 = bc^2 - hc^2 bh^2 = 169 - 25 = 144 bh = 12 (высота) медиана = высота = биссектриса (опущена на основание рб треугольника), значит bm = 1/2bh = 6

pumperdat

Математика

4,4(41 оценок)

Так как треугольник равнобедренный, то высота h к основанию является одновременно и медианой, и биссектрисой.поэтому все заданные точки лежат на этой высоте h. а) точка m пересечения медиан.высота h равна √(11²-(14/2)²) = √121 - 49) = √72 = 6√2. точка m пересечения медиан находится на расстоянии (2/3)h от вершины в: вм = (2/3)*6√2 = 4√2 ≈ 5,65685. б) точка о1 пересечения биссектрис. тангенс угла а равен: tg a = 6√2/7. тангенс половинного угла равен: tg(a/2) = tga/(1+√(1+tg²a)) = (6√2/7)/(1+√(1+(72/ = √2/3. искомое расстояние во1 = 6√2-(7*(√2/3)) = 11√2/3 ≈ 5,18545. в) точка о пересечения серединных перпендикуляров сторон. это расстояние равно: во = 5,5/cos (b/2) = 5,5/(6√2/11) = 60,5/(6√2) = 121/(12√2) ≈ 7,129993. г) точка h пересечения высот.вн находим из подобия взаимно перпендикулярных треугольников анд и вдс: вн = 6√2-(7*(7/6√2)) = 23/(6√2) ≈ 2,710576.(точка д - середина основания ас).

NELly1237

Математика

4,4(51 оценок)

нужно по делить или разделить

ответ:171 3/7

Если к неизвестном числу прибавить 7/18 того же числа, получится 66 2/3. Найдите это число

Реши свою проблему, спроси otvet5GPT

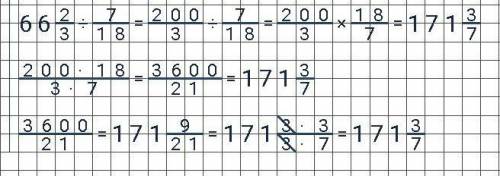
Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.