Регистрация Спросить otvet5GPT
vavilovaev86
11.01.2021 13:23
Алгебра
Есть ответ 👍

[является ли данная функция четной или нечетной]f(x)= \frac{1}{x-10}+ \frac{1}{x+20} [/tex]

148
379
Посмотреть ответы 2

Ответы на вопрос:

Lybava13322131
Lybava13322131
4,8(61 оценок)
F(-x)=1/(-x-10)+1/(20-x)=1/(20-x)-1/(x+10) функция не является четной-нечетной
Полькаа1642
Полькаа1642
4,8(24 оценок)

(-1,5; 3,25)

(1; 2)

Объяснение:

1.

{х+2у=5

{y=x^2+1

Нижнее уравнение подставляем в верхнее:

{х+2×(х^2+1)=5

{у=х^2+1

{2х^2+х+2=5

{у=х^2+1

{2х^2+х+2-5=0

{у=х^2+1

Находим корни квадратного

уравнения:

2х^2+х-3=0

а=2 в=1 с=-3

D=1-4×2×(-3)=1+24=25=5^2>0

x_1=(-1-5)/2×2=-6/4=-3/2=-1,5

x_2=(-1+5)/2×2=4/4=1

Подставляем найденные значе

ния х во второе уравнение:

у_1=х_1^2+1=

=(-1,5)^2+1=2,25+1=3,25

у_2=х_2^2+1=

=1^2+1=1+1=2

ответ записываем парами:

(х_1; у_1)

(х_2; у_2)

ответ: (-1,5; 3,25)

(1; 2)

Это же задание нужно выпол

нить графически.

2.

В первом уравнении системы

выразим у через х:

х+2у=5

2у=-х+5

у=(-х+5)/2=

=-х/2+5/2=-0,5х+2,5

Шаг 1.

Строим график функции

у=-0,5х+2,5

Так как функция линейная,

достаточно заполнить табли

цу для двух точек:

Х 1 3

У 2 1

Шаг 2.

Строим график квадратичной

функции:

у=х^2+1

а)

Можно воспользоваться шаб

лоном стандартной параболы

у=х^2

Вершина параболы находится

в точке начала отсчета (0; 0).

Ветви параболы направлены

вверх.

б)

С параллельного пе

реноса поднимаем параболу

у=х^2 вроль оси ОУ на 1ед.

Получили искомую параболу:

Вершина в точке (0; 1)

Ветви параболы направлены

вверх.

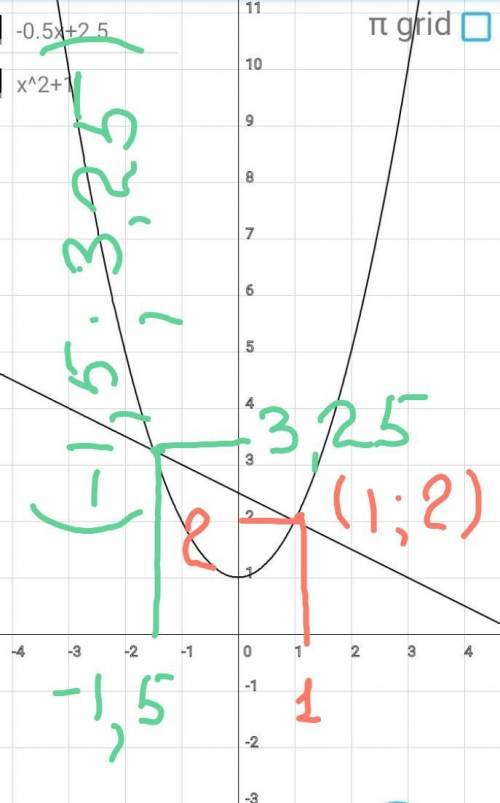
Шаг 3.

Определяем координаты точек

пкресечения прямой и парабо

лы:


Решите графическим и подстановки систему уравнений

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS