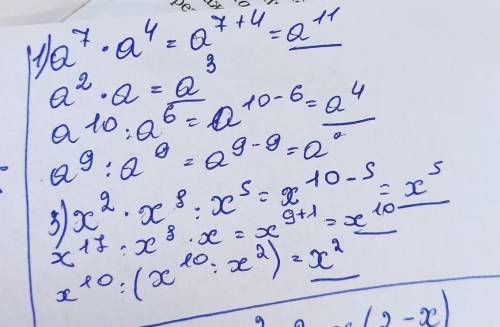Регистрация Спросить otvet5GPT
vasilprokofiev
27.03.2022 23:50
Алгебра
Есть ответ 👍

Найти промежутки возрастания и убывания функции f(x)=sinx-x f(x)=√(x²-1)

180
377
Посмотреть ответы 2

Ответы на вопрос:

chunya20041
chunya20041
4,6(79 оценок)
1) f(x) = sinx - x f'(x) = cosx - 1 f'(x)  ≥ 0 cosx - 1  ≥ 0 cosx  ≥ 1 неравенство обращается в равенство, т.к. cosx  ∈ [-1; 1]. отсюда делаем вывод, что функция убывает на всей своей области определения. ответ: убывает на r.  2) f(x) =  √(x² - 1) u = x² - 1, v =  √u f'(x) = u'·v' = (x² - 1)'·(√u)' = 2x·1/2√u = x/√(x² - 1) f'(x)  ≥ 0 x/[√x² - 1)  ≥ 0 знаменатель всегда больше нуля, т.к. подкоренное выражение - число неотрицательное. найдём d(y): x² - 1  ≥ 0 x  ∈ (-∞; -1] u [1; +∞). решаем далее неравенство: x  ≥ 0. с учётом области определения получаем, что при x  ∈ [1; +∞) функция будет возрастать (т.к. неравенство будет выполняться), а на (-∞; 1] функция будет убывать (т.к. неравенство не будет выполняться). ответ: убывает на (-∞; -1], возрастает на [1; +∞). 
ХозяинНосочков
ХозяинНосочков
4,5(5 оценок)

Объяснение:

вотт вроде так

ето только 1 и пол 3 задания


хелп если найдется человек который это сделает, то скиньте ответы в вк id:danila_hud​, если кто то р

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS