Вектор ab с началом в точке а(9; 2) имеет координаты (2; 6). найдите абсциссу точки в

182

232

Посмотреть ответы 2

Ответы на вопрос:

ТвояМилая

Геометрия

4,7(51 оценок)

→ а(х₁; у₁); в(х₂; у₂) ; ав{x₂ - x₁; y₂-y₁} решаем: → а(9; 2); в(х₂; у₂); ав {2; 6} x₂ - 9 = 2 x₂ =11 y₂ - 2 = 6 y₂ = 8 ответ: в(11; 8)

Slipknot55479876544

Геометрия

4,6(42 оценок)

Объяснение: в правильной 3-хугольной, 4-хугольной и 6-угольной призме все стороны основания равны. Для того чтобы найти объём каждой призмы воспользуемся формулой: V=Sосн×h, где h- её высота т.е. боковое ребро=12

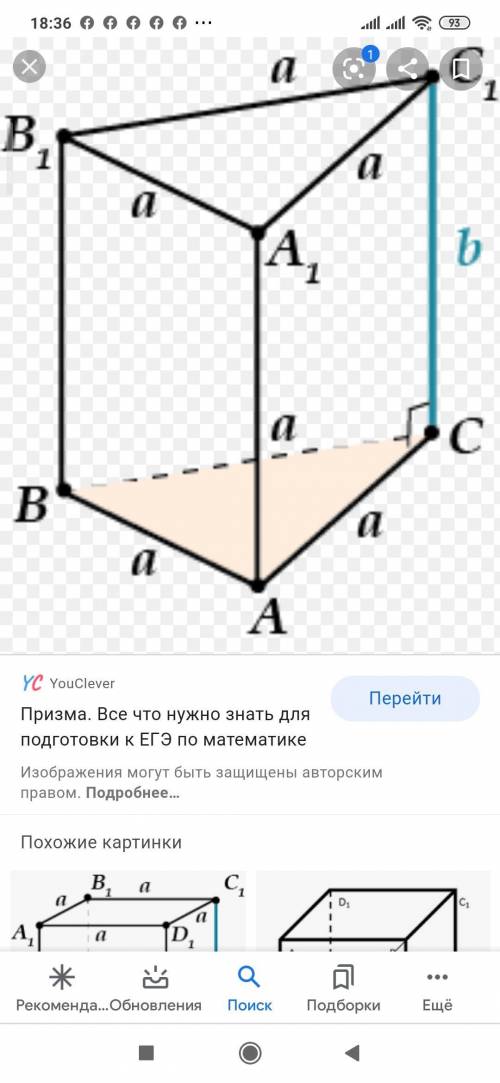
ЗАДАНИЕ 1

Найдём площадь основания 3-хугольной призмы, (где основанием является равносторонний треугольник) по формуле: S=a²√3/4, где а - сторона основания:

Sосн=10²√3/4=100√3/4=25√3(ед²)

Теперь найдём объем:

V=25√3×12=300(ед³)

ОТВЕТ: V=300(ед³)

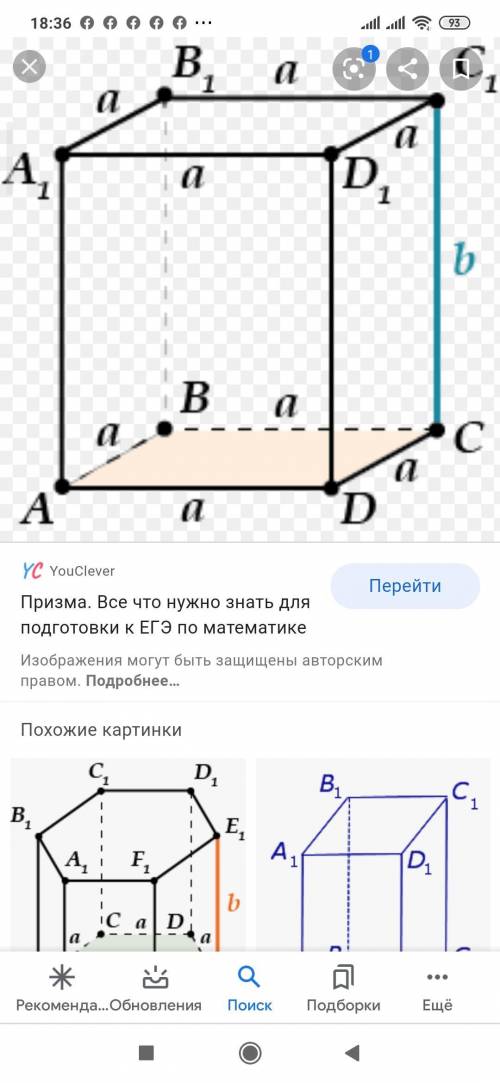
ЗАДАНИЕ 2

Так как в основании правильной четырёхугольной призмы лежит квадрат, то его площадь вычисляется по формуле: S=a², где а - его сторона:

Sосн=10²=100(ед²)

V=100×12=1200(ед³)

ОТВЕТ: V=1200(ед³)

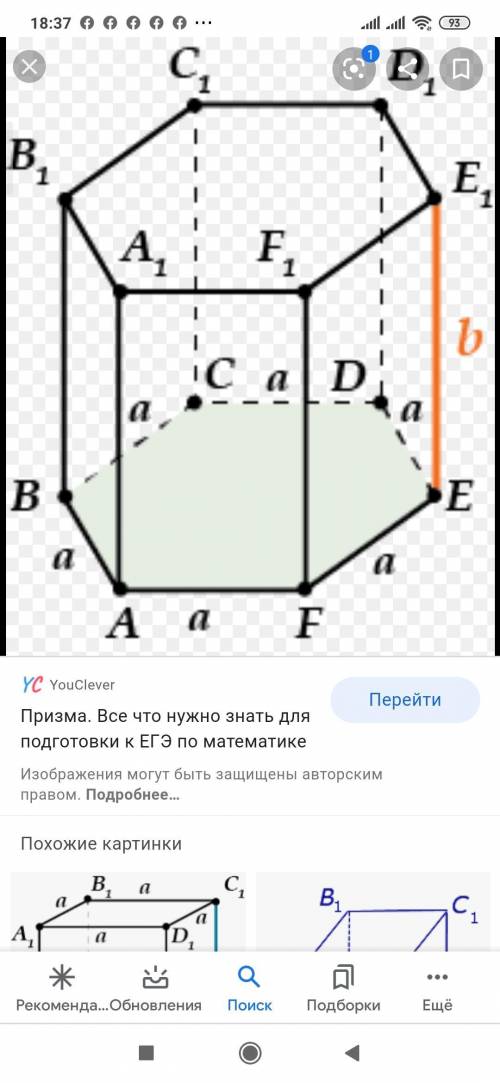
ЗАДАНИЕ 3

В основании правильной 6-угольной призмы лежит правильный шестиугольник. Его площадь состоит из 6 равносторонних треугольников. Найдём площадь одного такого треугольника по формуле:

S=a²√3/4=10²√3/4=100√3/4=25√3(ед²)

Так как таких треугольников 6 то, площадь основания=

Sосн=25√3×6=150√3(ед²)

Теперь найдём объем призмы:

V=150√3×12=1800(ед³)

ОТВЕТ: V=1800(ед³)

Сторона основания правильной призмы равна 10, боковое ребро равно 12. Найти объем треугольной, четыр

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.