18.05.2022 00:05

Есть ответ 👍

Решите уравнение 0,91: 3,64-0,8m=0,09

194

278

Посмотреть ответы 3

Ответы на вопрос:

НикаКлубника11

Математика

4,6(67 оценок)

0,91: 3,64-0,8m=0,09 91: 364=0,25(0,91 и 3,64 мы умножили на 100) получается 0,25-0,8m=0,09 -0,8m=0,09-0,25( получили 0,09-0,25 , потому что мы перенесли число в другую сторону ) -0,8m=-0,16 m = 0,16: 0,8 ( минусы ) m=0,2

Begzodik

Математика

4,8(43 оценок)

0,91: 3,64-0,8m=0,09 0,25-0,8m=0,09 -0,8m=0,09-0,25 -0,8m=-0,16 m=0,2

29101975tanuxa

Математика

4,5(21 оценок)

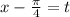
$x-\frac{\pi }{4}=t$

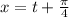
$x=t+\frac{\pi }{4}$

$x\rightarrow \frac{\pi}{4} ;t\rightarrow 0$

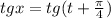
$tgx=tg(t+\frac{\pi}{4})$

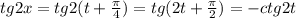
$tg2x=tg2(t+\frac{\pi}{4})=tg(2t+\frac{\pi}{2})=-ctg2t$

Обозначим:

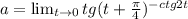
$a=\lim_{t \to 0} tg(t+\frac{\pi}{4})^{-ctg2t}$

Логарифмируем:

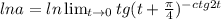
$lna=ln\lim_{t \to 0} tg(t+\frac{\pi}{4})^{-ctg2t}$

Знак предела и знак непрерывной функции можно менять местами:

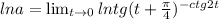
$lna=\lim_{t \to 0} lntg(t+\frac{\pi}{4})^{-ctg2t}$

Применяем свойство логарифма степени

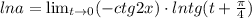
$lna=\lim_{t \to 0}(-ctg2x)\cdot lntg(t+\frac{\pi}{4})$

Запишем в виде дроби:

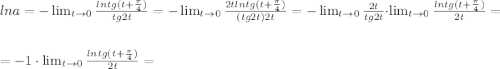
$lna=-\lim_{t \to 0}\frac{ lntg(t+\frac{\pi}{4})}{tg2t}=-\lim_{t \to 0}\frac{2t lntg(t+\frac{\pi}{4})}{(tg2t)2t}=- \lim_{t \to 0}\frac{2t}{tg2t}\cdot\lim_{t \to 0} \frac{ln tg (t+\frac{\pi}{4})}{2t} =\\\\=-1\cdot \lim_{t \to 0} \frac{ln tg (t+\frac{\pi}{4})}{2t} =$

неопределенность (0\0)= ( проще по правилу Лопиталя):

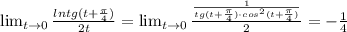
$\lim_{t \to 0} \frac{ln tg (t+\frac{\pi}{4})}{2t} = \lim_{t \to 0}\frac{\frac{1}{tg(t+\frac{\pi}{4})\cdot cos^2(t+\frac{\pi}{4} ) } }{2} =-\frac{1}{4}$

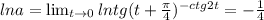
$lna=\lim_{t \to 0} lntg(t+\frac{\pi}{4})^{-ctg2t}=-\frac{1}{4}$

Значит,

$a=\lim_{t \to 0} tg(t+\frac{\pi}{4})^{-ctg2t}=e^{-\frac{1}{4}}=\frac{1}{\sqrt[4]{e}}$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.