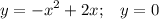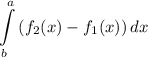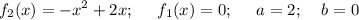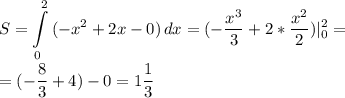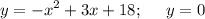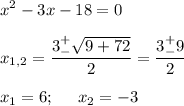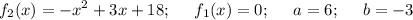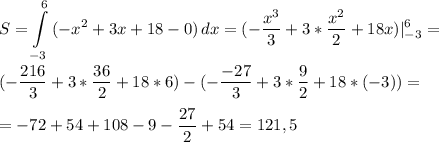Вшкольной лотерее 80 билетов,из них 20 выигрышных. какова вероятность проигрыша?
291
380
Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Найти значение выражения. 1/2+(0,3+1/2•3-(1+7/5): 2•1/2+3/2•2/3...
 Сергей1231819.07.2020 20:15
Сергей1231819.07.2020 20:15 -
Пароль для входа в программу состоит из 8 цифр. вова знает, что все цифры в пароле...
 123456789115517.10.2020 06:48
123456789115517.10.2020 06:48 -
Решить систему уравнений. х в квадрате + у в квадрате равно 13, ху=6...
 Germes1119.02.2022 13:56
Germes1119.02.2022 13:56 -
1.найдите значение производной функции y=-2cos3x в точке xo=0 2. найти значение...
 Kykyblohka24.05.2021 22:18
Kykyblohka24.05.2021 22:18 -
Постройте график функции y=|x-1|-|x+1|+x и найдите все значения k, при которых...
 whitesquirrelp06pc028.03.2023 03:06
whitesquirrelp06pc028.03.2023 03:06 -
Два трактора работая вместе могут вспахать поле за 2 дня. чтобы вспахать половину...
 Rovz18.09.2022 19:26
Rovz18.09.2022 19:26 -
1. Найди дискриминант квадратного уравнения 8x2+8x+12=0. ответ: D= 2. Определи...
 NoNaDa05.02.2023 12:32
NoNaDa05.02.2023 12:32 -
Реши систему уравнений методом подстановки. (-2 - 2 + 2 = 5 х = -6 — у ответ: 2...
 vasilchukanna117.02.2022 20:26
vasilchukanna117.02.2022 20:26 -
Реши систему уравнений методом подстановки: x — 2y = -14 7x – 12y = 7 ответ: (...
 alex0the0human02.11.2021 14:01
alex0the0human02.11.2021 14:01 -
Реши систему уравнений методом подстановки. (5 — 5(0,2y — 2и) = 3 (3u + 2) +2y...
 viktoriya22903.04.2020 15:46
viktoriya22903.04.2020 15:46

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.