Регистрация Спросить otvet5GPT
оуовлвдсл
01.03.2020 19:00
Алгебра
Есть ответ 👍

Решите уравнение где минус это степень 6-3 x 2-4 18-2

168
395
Посмотреть ответы 2

Ответы на вопрос:

islamsalpagaro
islamsalpagaro
4,4(6 оценок)
Тоесть 6х в 3 степени умножить на 2 в 4 степени?
maxcarleson1
maxcarleson1
4,7(57 оценок)

Объяснение:

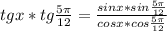
tgx*tg\frac{5\pi}{12} = \frac{sinx * sin\frac{5\pi}{12} }{cosx * cos\frac{5\pi }{12} }

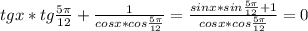
tgx*tg\frac{5\pi}{12} + \frac{1}{cosx*cos\frac{5\pi}{12} } = \frac{sinx*sin\frac{5\pi}{12}+1 }{cosx*cos\frac{5\pi}{12}} = 0

Домножим на знаменатель, избавившись, при условии, если:

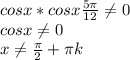cosx*cosx\frac{5\pi}{12} \neq 0\\ cosx \neq 0\\x \neq \frac{\pi }{2} + \pi kk ∈ Z - ОБЯЗАТЕЛЬНО указать

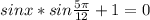
sinx*sin\frac{5\pi}{12} + 1 = 0

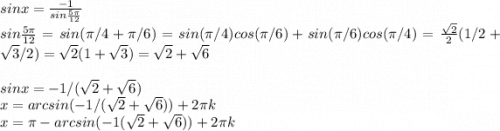
sinx = \frac{-1}{sin\frac{5\pi}{12} } \\sin\frac{5\pi}{12} = sin (\pi/4 + \pi/6) = sin(\pi/4)cos(\pi/6)+sin(\pi/6)cos(\pi/4) = \frac{\sqrt{2} }{2}(1/2 + \sqrt{3} / 2) = \sqrt{2}(1 + \sqrt{3}) = \sqrt{2} + \sqrt{6} \\\\sinx = -1/(\sqrt{2} + \sqrt{6})\\x = arcsin(-1/(\sqrt{2} + \sqrt{6})) + 2\pi k\\x = \pi - arcsin(-1(\sqrt{2} + \sqrt{6})) + 2\pi k

k ∈ Z

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS