Черничка21

16.03.2023 23:41

Геометрия

Есть ответ 👍

Угол при вершине равнобедренного треугольника равен b, а боковая сторона-b. найдите периметр треугольника.

131

375

Посмотреть ответы 2

Ответы на вопрос:

Динара22235

Геометрия

4,6(36 оценок)

Если мы проведем из вершины к основанию высоту, то она будет также биссектрисой и медианой. так как треугольник равнобедренный. будет образовано два прямоугльных треугольника. знаем, что боковая сторона = b, и знаем, что угол b поделится пополам изза биссектрисы. синус - это отношение противолежащего катета к гипотенузе, поэтому, так как медиана поделила основание пополам, половина основания/b=sin b/2 половина основания = b*sin b/2 полностью основание=2b*sin b/2 периметр = 2b+2b*sin b/2

Ivanka23

Геометрия

4,4(15 оценок)

Отрезки, на которые высота, проведенная с вершины тупого угла, делит большое основание равны 4 см и 14 см.

Объяснение:

Основы равнобедренной трапеции равны 10 см и 18 см. Найдите отрезки, на которые высота, проведенная с вершины тупого угла, делит большое основание.

Дано: ABCD - равнобедренная трапеция.

ВС = 10 см; AD = 18 см.

ВЕ - высота.

Найти: BC и AD.

Высота, опущенная из вершины тупого угла равнобедренной трапеции на большее основание, делит его на части, меньшая из которых равна полуразности оснований, а большая - полусумме оснований.

⇒ АЕ = (AD - BC) : 2 = (18 - 10) : 2 = 4 (см)

ED = (AD + BC) : 2 = (18 + 10) : 2 = 14 (см)

Докажем это свойство.

Пусть ВС = а, а AD = b.

Опустим еще один перпендикуляр CH на AD.

Рассмотрим ЕВСН.

ВС || EH (условие)

ВЕ ⊥ AD; CH ⊥ AD.

Если две прямые перпендикулярны третьей, то они параллельны между собой.

⇒ BE || CH.

ЕВСН - параллелограмм (по определению)

Все углы прямые.

⇒ ЕВСН - прямоугольник.

В прямоугольнике противоположные стороны равны.

⇒ ВС = ЕН = а

Рассмотрим ΔАВЕ и ΔHCD - прямоугольные.

АВ = CD (ABCD - равнобедренная трапеция)

Углы при основании равнобедренной трапеции равны.

∠A = ∠D

ΔАВЕ = ΔHCD (по гипотенузе и острому углу)

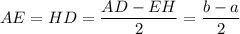
⇒ $\displaystyle AE = HD =\frac{AD-EH}{2} =\frac{b-a}{2}$

ED = HD + EH

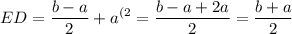
$\displaystyle ED = \frac{b-a}{2}+a^{(2}= \frac{b-a+2a}{2} =\frac{b+a}{2}$

Отрезки, на которые высота, проведенная с вершины тупого угла, делит большое основание равны 4 см и 14 см.

#SPJ1

Основи рівнобічної трапеції дорівнюють 10см та 18см. Знайдiть видризок, на якi висота, проведена з в

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.