Исследовать функцию с производной и построить ее график f(x)=2x^3-9x^2

224

326

Посмотреть ответы 2

Ответы на вопрос:

Егор111ив

Математика

4,5(78 оценок)

Исследуйте функцию и постройте ее график y= 2x³ - 9x² . 1.область определения функции d(f) = (-∞; ∞). 2. определяем точки пересечения графики функции с координатными осями a) c осью абсцисс : y =0 ⇒ 2x³ - 9x² = 0 , x²(2х - 9) = 0 ; имеем 2 корня: х = 0 и х = 9/2 = 4,5. a(0 ; 0) ; b(4,5 ; 0).b) с осью ординат: x =0 ⇒ y = 0 → а(0 ; 04). 3.определяем интервалы монотонности функции функция возрастает (↑), если у ' > 0, убывает(↓) , если у ' < 0. y ' =6x² - 18x =6x(x-3) ; y ' + - + 0 3 y ↑ max ↓ min ↑ x =0 точка максимума _ мах (у) = 0 x =3 точка минимума _ min (у) = 2*3³ - 9*3² = 54 - 81 = -27. функция возрастает , если x ∈(-∞ ; 0) и x ∈(3 ; ∞ ), убывает ,если x ∈ (0 ; 3 ). 4) определим точки перегиба , интервалы выпуклости и вогнутости y '' = (y ') ' =(6x² -18x) ' = 12x - 18 = 6(2x -3) .y '' =0 ⇒ x=3/2 =1,5 (единственная точка перегиба)график функции выпуклая , если y ''< 0 , т.е. если x < 1,5, вогнутая, если y '' > 0 ⇔ x > 1,5. 5. lim y → - ∞ ; lim y → ∞ x→ - ∞ x→ ∞

bastovayasofia

Математика

4,6(55 оценок)

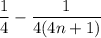
$\dfrac{1}{4}-\dfrac{1}{4(4n+1)}$

Пошаговое объяснение:

Попробуем представить дробь в виде суммы двух дробей:

$\dfrac{1}{(4n-3)(4n+1)}=\dfrac{A}{4n-3}+\dfrac{B}{4n+1}|\cdot(4n-3)(4n+1)\\1=A(4n+1)+B(4n-3)\\1=4An+A+4Bn-3B\\(4A+4B)n+A-3B=1$

В правой части нет членов с буквой n, то есть коэффициент перед n равен нулю, а свободный член равен одному:

$\displaystyle\left \{ {{4A+4B=0,} \atop {A-3B=1}} \right.\\\left \{ {{A=-B,} \atop {A+3A=1}} \right.\\\left \{ {{B=-\dfrac{1}{4},} \atop {A=\dfrac{1}{4}}} \right.$

Значит, $\dfrac{1}{(4n-3)(4n+1)}=\dfrac{1}{4(4n-3)}-\dfrac{1}{4(4n+1)}$

Таким образом, сумму можно представить, как

$\dfrac{1}{1\cdot5}+\dfrac{1}{5\cdot9}+...+\dfrac{1}{(4n-7)(4n-3)}+\dfrac{1}{(4n-3)(4n+1)}=\\=\dfrac{1}{4\cdot1}-\dfrac{1}{4\cdot5}+\dfrac{1}{4\cdot5}-\dfrac{1}{4\cdot9}+\dfrac{1}{4\cdot9}-...+\dfrac{1}{4(4n-7)}-\dfrac{1}{4(4n-3)}+\\+\dfrac{1}{4(4n-3)}-\dfrac{1}{4(4n+1)}=\dfrac{1}{4}-\dfrac{1}{4(4n+1)}$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.