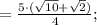Найдите первый член арифметической прогрессии (аn), если а13=68, d=-4,5

169

413

Посмотреть ответы 3

Ответы на вопрос:

lubenkovalilia2

Алгебра

4,5(19 оценок)

A13 = a1 + 12d = a1 + 12*(-4,5) = a1 - 54 = 68 a1 = 54 + 68 a1 = 122

uctni

Алгебра

4,6(15 оценок)

Решение: форумала а1=аn - (n-1)d a1=68-(13-1)×(-4,5)=122

gallavich2004

Алгебра

4,5(57 оценок)

$6-2\sqrt{7}; \quad \frac{5 \cdot (\sqrt{10}+\sqrt{2})}{4};$

Объяснение:

$\frac{4}{\sqrt{7}+3}=\frac{4 \cdot (\sqrt{7}-3)}{(\sqrt{7}+3) \cdot (\sqrt{7}-3)}=\frac{4 \cdot (\sqrt{7}-3)}{(\sqrt{7})^{2}-3^{2}}=\frac{4 \cdot (\sqrt{7}-3)}{7-9}=\frac{4 \cdot (\sqrt{7}-3)}{-2}=-2 \cdot (\sqrt{7}-3)=$

$=2 \cdot (3-\sqrt{7})=6-2\sqrt{7};$

$\frac{10}{\sqrt{10}-\sqrt{2}}=\frac{10 \cdot (\sqrt{10}+\sqrt{2})}{(\sqrt{10}-\sqrt{2})\cdot (\sqrt{10}+\sqrt{2})}=\frac{10 \cdot (\sqrt{10}+\sqrt{2})}{(\sqrt{10})^{2}-(\sqrt{2})^{2}}=\frac{10 \cdot (\sqrt{10}+\sqrt{2})}{10-2}=\frac{10 \cdot (\sqrt{10}+\sqrt{2})}{8}=$

$=\frac{5 \cdot (\sqrt{10}+\sqrt{2})}{4};$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Тамирис91
18.04.2023 08:34

{6x-2y-6=0 {5x-y-17=0 чему равна разность y-x?...
polcha2002
19.01.2021 05:13

Знайдіть розв язки нерівності 2х - 7х не профессорским решением...
АлинаSwons
11.06.2021 06:21

Розв язати нерівність -5х-2 3х топізде...
79954236
09.12.2020 18:34

Варiант 2 1. Закінчіть речення: Добуток думи двох вира на їх різницю дорівнює…...
nazarushka
11.04.2020 22:45

3tg(-п/3)*ctg п/3-sin п...
ксения1361
01.02.2020 09:58

с математикой, решите полностью...
HappyPerson23
17.09.2021 13:58

На рисунке- график производной функций. Найдите точку максимума функций...
демлан
16.05.2021 13:20

Примеры таких чисел а и b, что a b. изобразите их на координатной прямой....
АртёмПлотников
09.02.2021 02:46

Решите систему x^2+4xy-2y^2=5x+5y 5x^2-xy-y^2-7x=7y...
умник162д
06.06.2021 08:47

Решите неравенство интервалов: 7x-2/1-x больше или равно 0....

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.