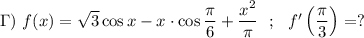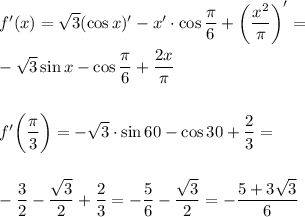Регистрация Спросить otvet5GPT
Гульдана111
16.08.2021 11:24
Математика
Есть ответ 👍

1)найти значение выражения 7/8+15/4: 10 /3 2)найти корень уравнения 1/кореньx=1/5

232
466
Посмотреть ответы 2

Ответы на вопрос:

vanya199jj
vanya199jj
4,4(68 оценок)
Решение- в приложении
kola3344
kola3344
4,5(73 оценок)

\mathrm{B)} ~~ 0 \Gamma) ~~ - \dfrac{5+ 3\sqrt{3} }{6}

Пошаговое объяснение:

Вспомним

(x^n)' = n \cdot x^{n-1} (u \pm v)' = u 'v \pm uv' (u\cdot v)' = u'v + uv' (C\cdot x )' = C (C\cdot f(x) ) ' = C \cdot f'(x) (C-const)

Тогда


\mathrm{B)} ~~ f(x) = x(1 + \cos x) ~~; ~~f(\pi ) = ?

f'(x) =x' (1+ \cos x ) + x(1+\cos x)' = 1 + \cos x -x \cdot \sin x f'(\pi ) = 1 + \cos \pi - \pi \cdot \sin \pi = 1- 1 -0 = 0


\Gamma ) ~ f(x) = \sqrt{3} \cos x - x\cdot \cos\dfrac{\pi }{6} + \dfrac{x^2}{\pi } ~~ ; ~~ f'\left(\dfrac{\pi }{3} \right) = ?


f'(x) = \sqrt{3} (\cos x) ' -x'\cdot \cos \dfrac{\pi }{6} + \left (\dfrac{x^2}{\pi } \right) ' = -\sqrt{3} \sin x - \cos \dfrac{\pi }{6} + \dfrac{2x}{\pi } f'\bigg(\dfrac{\pi }{3}\bigg ) = - \sqrt{3} \cdot \sin 60 - \cos 30 + \dfrac{2}{3} = - \dfrac{3}{2} - \dfrac{\sqrt{3} }{2 } + \dfrac{2}{3} = -\dfrac{5}{6} - \dfrac{\sqrt{3} }{2} = - \dfrac{5+ 3\sqrt{3} }{6}  

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS