Регистрация Спросить otvet5GPT
kostyabriakin
10.03.2023 07:43
Математика
Есть ответ 👍

Ширина прямоугольного ящика 8 сантиметров длина стороны квадратного ящика 32 сантиметра найди их периметр если известно что их площади равны.

300
500
Посмотреть ответы 3

Ответы на вопрос:

Annuta88
Annuta88
4,4(52 оценок)
32*32=160 ех короче это первое
KultchiK
KultchiK
4,4(86 оценок)
Площадь квадрата = сторона на сторону. 32*32=1024см.кв. площадь квадрата = площади прямоугольника. площадь прямоугольника = сторона на ширину. ширина- 8см, значит длина = 1024: 8=128см. периметр квадрата равен = 4*сторону квадрата = 4*32=128см. периметр прямоугольника = (длина + ширина) *2= (128+8)*2=136*2= 272см.
semabulov
semabulov
4,4(8 оценок)

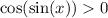
\cos( \sin(x) ) 0

Косинус больше нуля при таких значениях его аргумента:

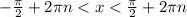
- \frac{\pi}{2} + 2\pi n < x < \frac{\pi}{2} + 2\pi n

В нашем случае его аргумент – синус, значит:

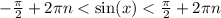
- \frac{\pi}{2} + 2\pi n < \sin(x) < \frac{\pi}{2} + 2\pi n

Синус существует в пределах от -1 до 1 включая концы. Переберём несколько значений n:

1. n = 0

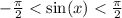
- \frac{\pi}{2} < \sin(x) < \frac{\pi}{2}

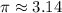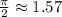Имеем ввиду, что \pi\approx 3.14, а \frac{\pi}{2} \approx 1.57. Поэтому для n = 0 неравенство выполняется для всех х;

2. n = -1:

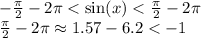
- \frac{\pi}{2} - 2\pi< \sin(x) < \frac{\pi}{2} - 2\pi \\ \frac{\pi}{2} - 2\pi \approx1.57 - 6.2 < - 1

Так как верхняя граница меньше -1, то нижняя и подавно, следовательно неравенство не выполняется.

3. n = 1:

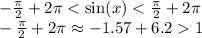
- \frac{\pi}{2} + 2\pi< \sin(x) < \frac{\pi}{2} + 2\pi \\ - \frac{\pi}{2} + 2\pi \approx - 1.57 + 6.2 1

В этом случае нижняя граница больше 1, а синус нестрого меньше 1, значит неравенство опять же не выполняется.

В итоге получили единственный случай при котором выполняется неравенство – при n = 0.

ответ: 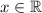x \in \mathbb R.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS