Регистрация Спросить otvet5GPT
taylakova090820
19.04.2020 19:30
Алгебра
Есть ответ 👍

Найти координаты вершины параболы y=-x^2+6x-5/ найти координаты точек пересечения с осями

228
428
Посмотреть ответы 2

Ответы на вопрос:

gggggerrrr
gggggerrrr
4,6(85 оценок)
Точки пересечения находятся через дискриминант д=16 х1=-1 х2=-5 это точки пересечения вершина находится по формуле -b/2a -6/2 равно -3 вершина) лучший ответ давай; )
лера2083
лера2083
4,7(57 оценок)

1. Белоснежка из семи гномов может выбрать любых двух, любых трех, любых четверых, любых пятерых, любых шестерых или всех семерых. Двух гномов можно выбрать 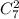C_7^2 трех - 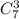C_7^3 и так далее до всех семи гномов, которых можно выбрать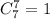 C_7^7=1

Тогда общее число можно рассчитать непосредственно как сумму:

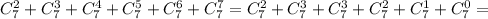
C_7^2+C_7^3+C_7^4+C_7^5+C_7^6+C_7^7=C_7^2+C_7^3+C_7^3+C_7^2+C_7^1+C_7^0=

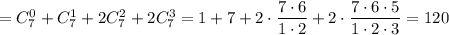
=C_7^0+C_7^1+2C_7^2+2C_7^3=1+7+2\cdot\dfrac{7\cdot6}{1\cdot2} +2\cdot\dfrac{7\cdot6\cdot5}{1\cdot2\cdot3}=120

Можно было воспользоваться интересным свойством для чисел сочетания:

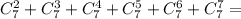
C_7^2+C_7^3+C_7^4+C_7^5+C_7^6+C_7^7=

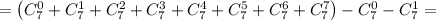
=\left(C_7^0+C_7^1+C_7^2+C_7^3+C_7^4+C_7^5+C_7^6+C_7^7\right)-C_7^0-C_7^1=

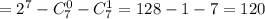
=2^7-C_7^0-C_7^1=128-1-7=120

ответ: 120

2. Рассмотрим ситуацию для слов длины 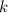k. Всего слов длины 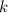k можно составить 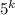5^k штук (или обозначая через размещения с повторениями 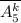\overline{A_5^k}). Слов длины 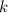k, не содержащих букву "г", можно составить 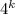4^k штук. Таким образом, слов длины 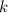k, содержащих букву "г" можно составить \left(5^k-4^k\right) штук.

Так как нас интересуют слова, с длиной не более 4 (то есть с длинами 1, 2, 3, 4), то необходимо вычислить следующую сумму:

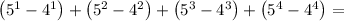
\left(5^1-4^1\right)+\left(5^2-4^2\right)+\left(5^3-4^3\right)+\left(5^4-4^4\right)=

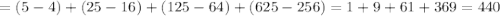
=(5-4)+(25-16)+(125-64)+(625-256)=1+9+61+369=440

ответ: 440

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS