Определить номер элемента, начиная с которого последовательность xn=2+7n-n^2 будет убывать. по-подробнее !
169
451
Ответы на вопрос:
Аналитическое решение: последовательность начнет убывать когда 2 + 7n будет меньше n^2 решим неравенство 2+7n < n^2 2+7n - n^2 < 0 найдем корни уравнения -x^2 + 7*x + 2 = 0 d = 49+8 = 57 x(1,2) = вычисляем и получаем 2 корня, -1, и 7. отрицательные корни нас не интересуют. а вот в точке 7.27 последовательность начинает убывать. значит номер элемента с которого последовательность начинает убывать: 8
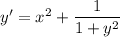
Решениями являются следующие пары:
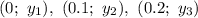
По условие уже известно, что 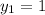
Для вычисления последующих значений 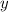 используем формулу:
используем формулу:
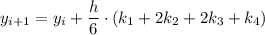 , где:
, где:
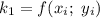
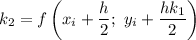
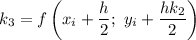
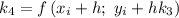
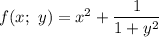
Рассчитываем 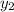 :
:
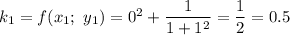
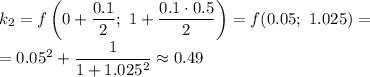
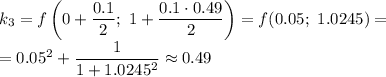
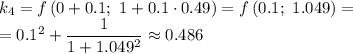
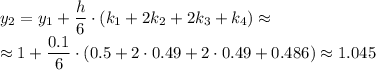
Рассчитываем 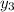 :
:
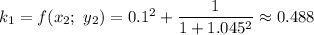
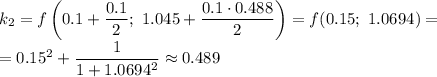
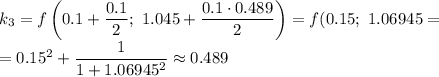
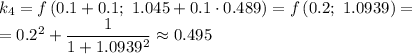
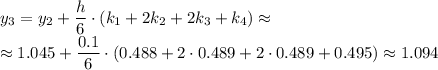
Приближенные решения:
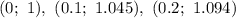
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Сделайте как можно быстрее...
 DashaLutova19.03.2021 05:00
DashaLutova19.03.2021 05:00 -
Решите уравнение: (х-1,5/14)-5/8=33/36...
 ЭлькаКотикучитсяна507.07.2021 02:51
ЭлькаКотикучитсяна507.07.2021 02:51 -
1)66а×(-8)= 2)4/7×(-49б)= Вычеслите...
 123456789085713.11.2021 22:01
123456789085713.11.2021 22:01 -
випадкова виличин Х має рівномірний закон розподілу на відрізку...
 Groyve116.06.2022 02:15
Groyve116.06.2022 02:15 -
Под номером 4, Где и какого типа разрывы имеет функция......
 10MisisVika1027.10.2020 07:20
10MisisVika1027.10.2020 07:20 -
5. Ребро куба 4 см. Если увеличить сторону куба на 2 см. Во сколько...
 nakiba32122.04.2023 05:00
nakiba32122.04.2023 05:00 -
Решите графическим систему уравнений: у – х = 2 у + х = 6...
 Zoomf15.05.2022 21:17
Zoomf15.05.2022 21:17 -
1. Решите систему уравнений по формуле Крамера 5х-8у=20 3х+2у=-22...
 shkolnig201302.01.2023 23:08
shkolnig201302.01.2023 23:08 -
Якій ліній відповідає рівняння 4x^2-2y^2-8-0 1)еліпс 2)парабола...
 tatsawi07.05.2023 08:49
tatsawi07.05.2023 08:49 -
раскройте скобки и упростите выражение: -(3,1c-6,7d)-(3d+1,2c)+-2,1c+1,3d)...
 Katerina932222.05.2021 18:28
Katerina932222.05.2021 18:28

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
