Геометрия: Напишите доклад на любую из тем или как доказывали

falala1

08.01.2023 00:56

Геометрия

Есть ответ 👍

Напишите доклад на любую из тем " " или " как доказывали "

103

421

Посмотреть ответы 2

Ответы на вопрос:

blazhenko66

Геометрия

4,5(76 оценок)

Лучше один раз увидеть, чем сто раз услышать. пословица. анри пуанкаре сказал, что — это искусство называть разные вещи одина- ковыми именами. осмелимся добавить: а одинаковые вещи — разными именами. то есть один и тот же объект можно описывать на разных языках, видеть разными глазами. при этом непонятное ранее утверждение может стать очевидным, а к сложной может отыскаться лёгкое решение. на школьном уровне эта идея обычно реализуется как перевод на язык арифме- тических (текстовые решают с уравнений) и (координатный и векторный методы). такой перевод позволяет алгоритмизировать реше- ние . заметим, что алгоритмизация не всегда полезна: не нужно ничего изобретать, решение идёт по накатанной схеме. “решать с уравнений , допускающую простое арифметическое решение, безнравственно.” [1, с. 46] менее известны другие случаи, когда арифметические и удобно решать на языке. таким примерам и посвящена эта статья. доказать значит сделать очевидным ключевые факты полезно формулировать на разных языках, чтобы каждый ученик усваивал их на свойственном ему языке. для многих вовремя показанная картинка может раз и навсегда навести ясность и спасти от типичных ошибок. 1. переместительный закон сложения для положительных чисел можно пояснять так: поезд проехал a км от москвы до твери и b км от твери до петербурга. на обратном пути он проехал те же расстояния в обратном порядке, и общий путь был тот же самый. значит, a + b = b + a. переместительный закон сложения для целых чисел хорошо пояснять с дви- жения лифта. например, (+3) + (−5) означает, что лифт поехал сначала на 3 этажа вверх, а потом на 5 вниз. а (−5) + (+3) означает, что лифт сначала поехал на 5 этажей вниз, а потом на 3 вверх. ясно, что в итоге он переместился на одно и то же число этажей в одну и ту же сторону3. тот же пуанкаре говорил, что научиться складывать дроби можно двумя способами: разрезая яблоки и . . разрезая пироги. в статье и на доске проще резать прямоугольники (“шоколадки”), но суть будет та жеспросите пятиклассника, чему равен квадрат суммы — и он наверняка ответит “сумме квадратов”. переубедить его проще всего с картинки 6: считаем площадь боль- шого квадрата двумя способами. говорят, когда руссо учился в школе, его убедило только такое доказательство. можно придумать картинки для доказательства разложения квад- рата суммы трёх слагаемых, для разности квадратов и даже для куба суммы [2]. правда, последнее является скорее тренировкой пространственного воображения, но это тоже по- лезно. 5. формула для производной произведения двух функций, как и формула суммы квад- ратов, не принадлежит к числу интуитивно ясных: хочется по аналогии с производнойсуммы сказать “равна произведению производных”. в эту ловушку попался сначала да- же. . лейбниц, один из создателей дифференциального исчисления.

dimon007228

Геометрия

4,7(49 оценок)

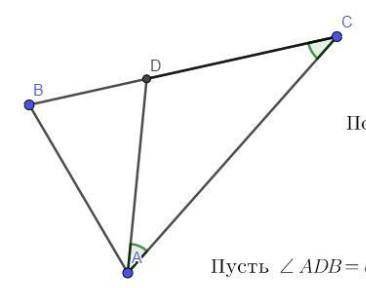
По свойству биссектрисы: 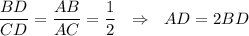$\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{1}{2}~~\Rightarrow~~AD=2BD$ .

Обозначим 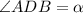$\angle ADB=\alpha$ , тогда 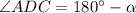$\angle ADC=180^\circ -\alpha$ (как смежные).

Далее воспользуемся теоремой косинусов для треугольников BDA и ADC, мы имеем:

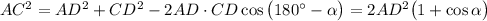
$AC^2=AD^2+CD^2-2AD\cdot CD\cos \big(180^\circ -\alpha\big)=2AD^2\big(1+\cos \alpha\big)$

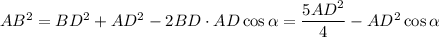
$AB^2=BD^2+AD^2-2BD\cdot AD\cos \alpha =\dfrac{5AD^2}{4}-AD^2\cos \alpha$

Второе равенство подставляем в первое, приняв во внимая AC=2AB

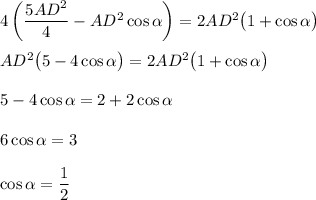
$4\left(\dfrac{5AD^2}{4}-AD^2\cos \alpha\right)=2AD^2\big(1+\cos \alpha\big)\\ \\ AD^2\big(5-4\cos \alpha\big)=2AD^2\big(1+\cos \alpha\big)\\ \\ 5-4\cos \alpha=2+2\cos \alpha\\ \\ 6\cos \alpha=3\\ \\ \cos \alpha=\dfrac{1}{2}$

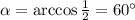
$\alpha =\arccos\frac{1}{2}=60^\circ$

ответ: 60 градусов.

Биссектриса AD треугольника ABC равна отрезку DC, AC=2AB. Найдите величину угла ADB в градусах.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.