Регистрация Спросить otvet5GPT
galaninartem201
28.03.2023 01:53
Геометрия
Есть ответ 👍

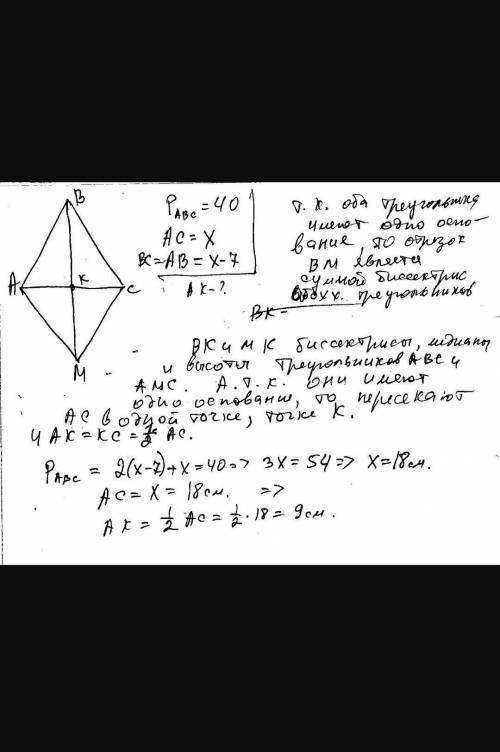
Даны координаты вершин треугольника авс найти длину стороны ав, уравнение сторон ав и вс и их угловых коэффициентов, внутренний угол в в радиусах с точностью до двух знаков, уравнение высоты сд и её длину, уравнение медианы ае и координаты точки к пересечение этой медианы с высотой сд, уравнение прямой проходящей через точку к параллельной стороне ав, координаты точки м расположенной симметрично прямой сд а(2; 5) в(14; -4) с(18; 18)

186
212
Посмотреть ответы 2

Ответы на вопрос:

Gusein123
Gusein123
4,5(1 оценок)
1) ав =√((14-2)²+)-5)²) =  √(144+81) =  √225 = 15. 2)  это каноническое уравнение прямой ав, оно же в общем виде: -9х + 18 = 12у - 60, 9х +12у - 78 = 0,   3х + 4у - 26 = 0 или в виде уравнения с коэффициентом: у = (-9/12)х  +  (78/12) = (-3/4)х + 13/2 = -0,75х + 6,5. вс: (х-14)/(18-14) = (у+4)/(18+4), вс: (х-14)/4 = (у+4)/22 (если уравнения нужны в другом виде - то по аналогии с ав самому пересчитать). угловые коэффициенты находятся при пересчёте уравнения с коэффициентом: ав: к=-0,75,                           вс:   у = 5,5 х -  81     к = 5,5.3)  cos в=  (ав²+вс²-ас²) / (2*ав*вс)   = 0,447214.      b = 1,107149 радиан = 63,43495 градусов.4) сд:     (х-хс)/(ув-уа)     =  (у-ус)/(ха-хв). расчет длин сторон: ав = √((хв-ха)²+(ув-уа)²) =  √225 =  15.  bc = √((хc-хв)²+(ус-ув)²) =  √500 =  22,360679.ac = √((хc-хa)²+(ус-уa)²) =  √425 =  20,61552813.  полупериметр р = 28,98810,   s =  √(p(p-a)(p-b)(p-c)) =  150.площадь можно определить и по другой формуле: s=(1/2)*|(хв-ха)*(ус--ха)*(ув-уа)| = 150.длина высоты сд =  2s/ав = 20.       
Celestialess32
Celestialess32
4,5(23 оценок)

ответ на фото

Объяснение:

ответ на фото


На стороне АС как на основании по разные стороны от неё построены два равнобедренных треугольника АВ

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS