NastikLoVe22

22.07.2022 03:49

Геометрия

Есть ответ 👍

Втреугольнике abc угол c равен 75° , а угол b равен 60°. вершина m равнобедренного прямоугольного треугольника bcm с гиптенузой bc расположена внутри треугольника abc.найдите угол mac.

136

482

Посмотреть ответы 2

Ответы на вопрос:

Германкорпорация

Геометрия

4,8(40 оценок)

Угол baс = 45 гр. проведём окружность с центром м и радиусов мв=мс. т.к. угол вмс = 90 гр, то большая дуга вс этой окружности является местом точек, из которых хорда вс видна под углом 45 гр. следовательно, вершина а принадлежит этой окружности. значит треугольник амс - равнобедренный, и следовательно угол мас= углу мса= углу вса - (минус) угол мсв = 75 гр- 45 гр = 30 гр.

05Adam05

Геометрия

4,8(5 оценок)

ответ:

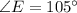
$\angle E=105^{\circ}$

Объяснение:

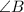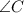Проведём биссектрисы $\angle B$ и $\angle C$ . Пусть они пересекаются в точке .

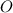Также проведём прямые 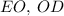$EO, \: OD$ и .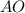

========================================

Рассмотрим 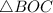$\triangle BOC$ :

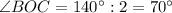$\angle BOC = 140^{\circ}:2=70^{\circ}$ , т.к. 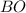- биссектриса.

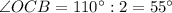$\angle OCB=110^{\circ}:2=55^{\circ}$ , т.к. 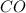- биссектриса.

Сумма внутренних углов треугольника равна 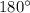$180^{\circ}$ .

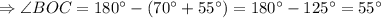
$\Rightarrow \angle BOC=180^{\circ}-(70^{\circ}+55^{\circ})=180^{\circ}-125^{\circ}=55^{\circ}$

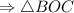$\Rightarrow \triangle BOC$ - равнобедренный.

========================================

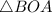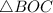Рассмотрим $\triangle BOA$ и $\triangle BOC$ :

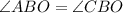$\angle ABO=\angle CBO$ , т.к. 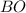- биссектриса;

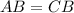AB=CB (по условию); 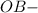OB - общая сторона.

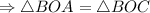$\Rightarrow \triangle BOA=\triangle BOC$ (по I признаку равенства треугольников).

========================================

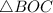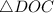Рассмотрим $\triangle BOC$ и $\triangle DOC$ :

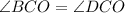$\angle BCO=\angle DCO$ , т.к. 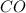- биссектриса;

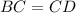BC=CD (по условию), 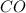- общая сторона.

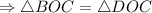$\Rightarrow \triangle BOC=\triangle DOC$ (по I признаку равенства треугольников).

========================================

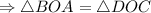$\Rightarrow \triangle BOA=\triangle DOC$ , т.е. мы имеем три равных равнобедренных тр-ка:

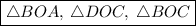
$\boxed{\triangle BOA, \: \triangle DOC,\: \triangle BOC}$

========================================

Рассмотрим 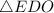$\triangle EDO$ :

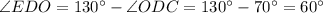$\angle EDO=130^{\circ}-\angle ODC=130^{\circ}-70^{\circ}=60^{\circ}$ .

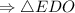$\Rightarrow \triangle EDO$ - равносторонний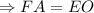 $\Rightarrow FA=EO$

========================================

Рассмотрим геометрическую фигуру 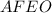AFEO :

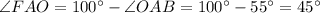$\angle FAO=100^{\circ}-\angle OAB=100^{\circ}-55^{\circ}=45^{\circ}$ .

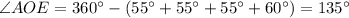$\angle AOE=360^{\circ}-(55^{\circ}+55^{\circ}+55^{\circ}+60^{\circ})=135^{\circ}$ (т.к. в полном угле всего 360°)

При пересечении двух параллельных прямых секущей, сумма односторонних углов равна 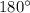$180^{\circ}$ .

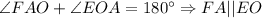
$\angle FAO+\angle EOA=180^{\circ} \Rightarrow FA|| EO$

Если у геометрической фигуры есть 4 угла, 4 стороны, а 2 стороны равны и параллельны, то этот четырёхугольник - параллелограмм.

У параллелограмма противоположные углы равны.

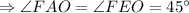$\Rightarrow \angle FAO=\angle FEO=45^{\circ}$ .

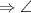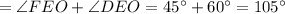
$\Rightarrow \angle$ DEF $=\angle FEO+\angle DEO=45^{\circ}+60^{\circ}=105^{\circ}$

========================================

В шестиугольнике ABCDEF выполнены равенства FA=AB=BC=CD=DE, ∠A=100∘, ∠B=140∘, ∠C=110∘, ∠D=130∘. Найд

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.