Впрямоугольном треугольнике abc уголb=90градусов,ab=3см,угол c=25градусов.найт углы и стороны.

203

371

Посмотреть ответы 2

Ответы на вопрос:

kseniatrof

Геометрия

4,5(21 оценок)

Угол а будет равен 65 градусов т,к все углы треугольника в сумме 180 градусов а значит: 180=в+с+а. а=180-(в+с). а=180-(90+25). а=180-115.а=65 градусов. со сторонами попозже на листочке скину так как тут нужно подумать

Anonim30001

Геометрия

4,6(66 оценок)

Даны вектора а(2;-2;1) , b(8;4;1). Найти площадь треугольника, построенного на векторах 2а и b.

Объяснение:

S=1/2*a*b*sin(a;b), где а и b стороны треугольника.

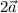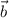Сторонами треугольника будут отрезки на которых лежат вектора $\displaystyle 2\vec{a}$ и $\displaystyle \vec{b}$ .

Найдем координаты вектора 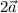$\displaystyle 2\vec{a}$ (2*2;-2*2;1*2 ) или 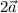$\displaystyle 2\vec{a}$ (4;-4;2 ).

Длина 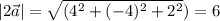$\displaystyle |2\vec{a}|=\sqrt{(4^{2} +(-4)^{2}+2^{2} }) =6$

Длина 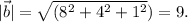$\displaystyle |\vec{b}|=\sqrt{(8^{2} +4^{2}+1^{2} }) =9.$ /

Найдем угол между ними по формуле 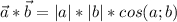$\displaystyle \vec{a}*\vec{b}=|a|*|b|*cos(a;b)$

4*8-4*4+2*1=6*9*cosα ⇒ cosα=18/54 ,cosα=1/3.

По основному тригонометрическому тождеству

sinα=√(1-1/9)=(2√2)/3

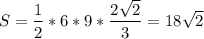$\displaystyle S=1/2* |2\vec{a}|* |\vec{b}|*sin(a;b),$ $\displaystyle S=\frac{1}{2} * 6*9*\frac{2\sqrt{2} }{3} =18\sqrt{2}$ ( ед²)

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.