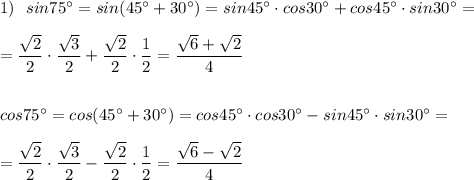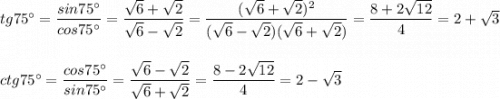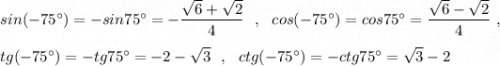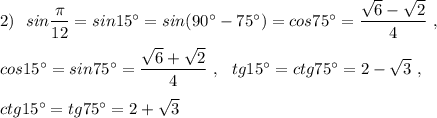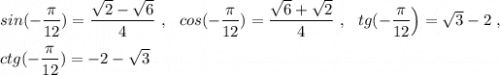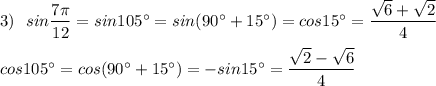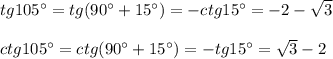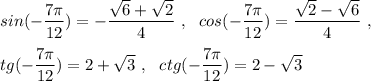Разложите многочлен на множители с фсу: 1. 1-m^2-2mn-n^2 2.16-(x^2-2xy+y^2)
169
324
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Представь 2⁵⁶ в виде степени с основанием 2²⁸...
 Shaman1223304.03.2020 14:14
Shaman1223304.03.2020 14:14 -
если не сделаю это, по алгебре выйдет двойка... ...
 Kirpiche30.04.2020 01:31
Kirpiche30.04.2020 01:31 -
ответ и решение запишите на листике , и прикрепите в ответ Кто умеет...
 аля66816.07.2022 18:31
аля66816.07.2022 18:31 -
В формуле D=S-P, -называется. а.процентной ставкой. б.наращенной суммой....
 jullii5501.02.2020 12:20
jullii5501.02.2020 12:20 -
Разложите на множители квадратный трехчлен ( через дискриминант ):...
 Konfetaz22.06.2022 07:10
Konfetaz22.06.2022 07:10 -
Подайте одночлен 16х12у8 у вигляді: б) добутку двох одночленів, одним...
 Миша111299419.10.2021 11:08
Миша111299419.10.2021 11:08 -
Знайдіть точку максимума функции f(x)=-6x в квадрате +x в кубе...
 slava4В09.08.2020 16:37
slava4В09.08.2020 16:37 -
1. вычислите sin t и cos t, если а) t=5п/6; б) t=5п/4; в) t= 7п/6;...
 nina23609.06.2020 04:50
nina23609.06.2020 04:50 -
Как построить график функции, заданной формулой. например у= -2х+1...
 Amanda17313.10.2022 22:18
Amanda17313.10.2022 22:18 -
Определите наименьшее значение функции y=12 sinx на отрезке [-п/12;...
 t11o23.01.2022 04:42
t11o23.01.2022 04:42

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.