Решить ! стороны перпендикулярного сечения наклонной треугольной призмы относятся, как 12: 17: 25, боковое ребро равно 15 дм. зная что площадь перпендикулярного сечения равна 360 дм2. найти боковую поверхность призмы.

Стороны треугольника в перпендикулярном сечении будут высотами параллелограммов, составляющих боковую поверхность. поэтому надо найти периметр этого треугольника, и умножить его на длину бокового ребра 15, получится ответ. 1) для начала надо внимательно рассмотреть треугольник со сторонами 12, 17, 25. этот треугольник подобен перпендикулярному сечению. площадь такого треугольника равна 90. это просто сосчитать по формуле герона. p = (12 + 17 + 25)/2 = 27; p - 12 = 15; p - 17 = 10; p - 25 = 2; s^2 = 27*15*10*2 = (9*5*2)^2 = 90^2; s = 90; (само собой, лично я ничего такого не делал, что же я, совсем глупый, что-ли? - по формуле герона этот треугольник очевидно равен "разности" двух пифагоровых треугольников - со сторонами (15, 20, 25) и (8, 15, 17), поэтому высота к стороне 12 равна 15, и площадь 12*15/2 = 90; даже ручка не 2) по условию, площадь перпендикулярного сечения в 4 раза больше, поэтому его стороны больше в 2 раза, и периметр - тоже. p = (12 + 17 + 25)*2 = 108; 3) площадь боковой поверхности призмы 108*15 = 1620;

8 2/3 см;  8 2/3 см;  13 2/3 см

Объяснение:

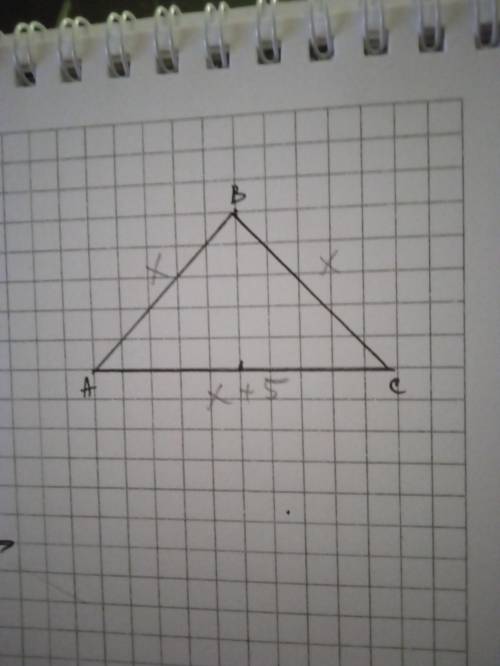
Дано: ΔАВС - равнобедренный;  АВ=ВС;  АС-АВ=5 см.  АВ - ? ВС - ?  АС - ?

Пусть АВ=ВС=х см, тогда АС=х+5 см.

х+х+х+5=31

3х=26

х=8  2/3

АВ=ВС=8  2/3 см;  АС=8  2/3 + 5 = 13  2/3 см