Регистрация Спросить otvet5GPT
филик2
30.11.2022 20:36
Алгебра
Есть ответ 👍

Найдите производную функции f (х) = и вычислите ее значение в точке х₀ = 1.

157
456
Посмотреть ответы 2

Ответы на вопрос:

LikiMikhoelis
LikiMikhoelis
4,6(47 оценок)
Решение f `(x) = [2x*(3x - 1) - 3*(x² - 4)] / (3x - 1)² =  = (6x² - 2x - 3x² + 12) /  (3x - 1)² = (3x² - 2x + 12) /  (3x - 1)²   x₀ = 1 f`(1) = (3 - 2 + 12) / (3 - 1)² = 13 / 4 = 3,25
ученица2002222
ученица2002222
4,4(53 оценок)

Пользуемся формулами приведения , формулами суммы и разности тригонометрических функций .

\boxed {\ sin(\alpha \pm \beta )=sin\alpha \, cos\beta \pm cos\alpha \, sin\beta \ }boxed{\ cos(\alpha \pm \beta )=cos\alpha \, cos\beta \mp sin\alpha \, sin\beta \ }

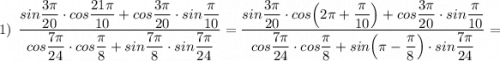
\displaystyle 1)\ \ \frac{sin\dfrac{3\pi}{20}\cdot cos\dfrac{21\pi }{10}+cos\dfrac{3\pi}{20}\cdot sin\dfrac{\pi}{10} }{cos\dfrac{7\pi}{24}\cdot cos\dfrac{\pi}{8}+sin\dfrac{7\pi}{8}\cdot sin\dfrac{7\pi }{24}}=\frac{sin\dfrac{3\pi}{20}\cdot cos\Big(2\pi +\dfrac{\pi }{10}\Big)+cos\dfrac{3\pi}{20}\cdot sin\dfrac{\pi}{10} }{cos\dfrac{7\pi}{24}\cdot cos\dfrac{\pi}{8}+sin\Big(\pi -\dfrac{\pi}{8}\Big)\cdot sin\dfrac{7\pi }{24}}=

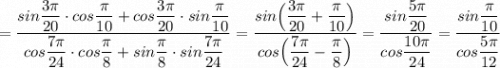
= \dfrac{sin\dfrac{3\pi}{20}\cdot cos\dfrac{\pi }{10}+cos\dfrac{3\pi}{20}\cdot sin\dfrac{\pi}{10} }{cos\dfrac{7\pi}{24}\cdot cos\dfrac{\pi}{8}+sin\dfrac{\pi}{8}\cdot sin\dfrac{7\pi }{24}}=\dfrac{sin\Big(\dfrac{3\pi}{20}+\dfrac{\pi}{10}\Big)}{cos\Big(\dfrac{7\pi }{24}-\dfrac{\pi}{8} \Big)}=\dfrac{sin\dfrac{5\pi}{20}}{cos\dfrac{10\pi}{24}}=\dfrac{sin\dfrac{\pi}{10}}{cos\dfrac{5\pi}{12}}

Значения 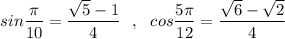  sin\dfrac{\pi }{10}=\dfrac{\sqrt5-1}{4}\ \ ,\ \ cos\dfrac{5\pi }{12}=\dfrac{\sqrt6-\sqrt2}{4}  , тогда в результате

получим 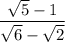   \dfrac{\sqrt5-1}{\sqrt6-\sqrt2}  .

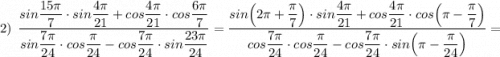
\displaystyle 2)\ \ \frac{sin\dfrac{15\pi}{7}\cdot sin\dfrac{4\pi }{21}+cos\dfrac{4\pi}{21}\cdot cos\dfrac{6\pi}{7} }{sin\dfrac{7\pi}{24}\cdot cos\dfrac{\pi}{24}-cos\dfrac{7\pi}{24}\cdot sin\dfrac{23\pi }{24}}=\frac{sin\Big(2\pi +\dfrac{\pi}{7}\Big)\cdot sin\dfrac{4\pi }{21}+cos\dfrac{4\pi}{21}\cdot cos\Big(\pi -\dfrac{\pi}{7}\Big)}{cos\dfrac{7\pi}{24}\cdot cos\dfrac{\pi}{24}-cos\dfrac{7\pi}{24}\cdot sin\Big(\pi -\dfrac{\pi }{24}\Big)}=

=\dfrac{sin\dfrac{\pi}{7}\cdot sin\dfrac{4\pi }{21}-cos\dfrac{4\pi}{21}\cdot cos\dfrac{\pi}{7} }{sin\dfrac{7\pi}{24}\cdot cos\dfrac{\pi}{24}-cos\dfrac{7\pi}{24}\cdot sin\dfrac{\pi }{24}}=\dfrac{-cos\Big(\dfrac{\pi}{7}+\dfrac{4\pi}{21}\Big)}{sin\Big(\dfrac{7\pi }{24}-\dfrac{\pi}{24}\Big)}=\dfrac{-cos\dfrac{7\pi}{21}}{sin\dfrac{6\pi}{24}}=\dfrac{-cos\dfrac{\pi}{3}}{sin\dfrac{\pi}{4}}==\dfrac{\dfrac{1}{2}}{\dfrac{\sqrt2}{2}} =\dfrac{1}{\sqrt2}=\dfrac{\sqrt2}{2}

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS