Регистрация Спросить otvet5GPT
OVRBTZ
19.09.2022 04:15
Алгебра
Есть ответ 👍

Решите уравнение l(x-1)²-4l=4-(1-x)²

280
399
Посмотреть ответы 2

Ответы на вопрос:

alieismailova1
alieismailova1
4,7(96 оценок)
По определению модуля: ( x - 1)^2 - 4 = 4 - ( 1 - x)^2   или   ( x - 1)^2 - 4 = - (4 -(1 - x)^2) x^2 - 2x + 1 - 4 = 4 -(1 - 2x+x^2)     x^2-2x+1-4= -(4 -(1-2x+x^2) x^2 - 2x - 3 - 3 - 2x + x^2=0             x^2-2x-3=- (3+2x-x^2) 2x^2 - 4x - 6 = 0                               x^2 - 2x-3= - 3 - 2x + x^2 x^2 - 2x - 3= 0                                   x^2 - x^2 - 2x+ 2x = - 3+3 d = b^2 - 4ac = 4+12=16                 0x = 0 - имеет бесконечное множество x1 = (2 + 4)/2 = 3                               решений x2 = ( 2 - 4)/ 2 = - 1
braununs
braununs
4,7(74 оценок)

Так как существует конечный предел

\[\mathop {\lim }\limits_{x \to x_0 } \frac{{f(x) - f(x_0 )}}{{x - x_0 }} = k\]

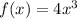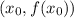То график функции f(x)=4x^3 имеет касательную в точке (x_0,f(x_0)).

Запишем уравнение касательной в общем виде

\[Y = k(X - x_o ) + f(x_0 )\]

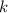Где k - угловой коэффициент касательной. Очевидно, что равен производной функции 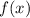f(x)\\ (геометрический смысл производной).

Найдем производную это функции с определения

\[f'(x) = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f(x + \Delta x) - f(x)}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{4\left[ {x + \Delta x} \right]^3 - 4x^3 }}{{\Delta x}} = 12x^2 \]

Производная в точке x0, равна

\[f'(x_0 ) = 12 \cdot 7^2 = 588\]

Вычислим значение функции в точке x0=7

\[f(x_0 ) = 4 \cdot 7^3 = 1372\]

Тогда уравнение касательной имеет вид

\[Y = 588\left[ {X - 7} \right] + 1372 = 588X - 2744\]

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS