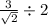"синус, косинус и тангенс углов 30°, 45° и 60°" решите 1. стороны параллелограмма равны 8 и 10 см, угол между ними 60°. найдите площадь параллелограмма. 2. найдите площадь параллелограмма, у которого стороны равны 8 и 6 см, а угол равен 45°. 3. в прямоугольной трапеции меньшее основание равно 6, а меньшая боковая сторона равна 2√3. найдите площадь трапеции, если один из её углов равен 120°. 4. в равнобедренной трапеции меньшее основание равно 5, а высота равна √3. найдите площадь трапеции, если один из её углов равен 150°.

192

455

Посмотреть ответы 2

Ответы на вопрос:

алгебра107

Геометрия

4,5(69 оценок)

1.)s=a*b*sin a

s=8*10*sin 60=80*sqrt(3)/2=40sqrt(3)

sqrt(3) корень квадратный

2.)s параллелограмма = 2s треугольника = 2 * 1/2 * a * b * sin a = 8 * 6 * sin 45 = 48 * √2/2 = 24√2

3.)пусть авсd - данная трапеция, ab=6, ad=2*корень(3), угол авс=120 градусов,

проведем высоту вк

тогда угол kbc=120-90=30 градусов

угол с=90-30=60 градусов

bk=ad=2*корень(3)

dk=ab=6

по соотношениям в прямоугольном треугольнике

bk/ck=tg c

ск=bk/ tg c

ck=2*корень(3)/tg 60=2*корень(3)/корень(3)=2

cd=ck+dk=6+2=8

площадь трапеции равна произведению ее высоту на полусумму ее оснований

s=(ab+cd)/2 *ad

s=(6+8)/2*2*корень(3)=14*корень(3)

4.)роведём высоту из верхнего угла на нижнее основание - в точку к

оба нижних угла будут = 180 - 150 = 30 гр тангенс 30 = 1/корень из 3 отрезок ак = высота / тангенс 30 = 3 нижнее основание = 3+5+3 = 11 средняя линия = (11 +5) /2 = 8 площадь = 8 * корень из 3

Анастасия5451

Геометрия

4,8(26 оценок)

90 +60=150 180 - 150=130

Угол а =30

$\frac{3}{ \sqrt{2} } \div 2$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.