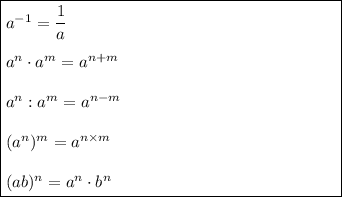Найдите промежутки возрастания и убывания функции определите ее точки экстремума: а)f(x)=2x-5 б)f(x)=x^+4x+5 в)f(x)=x^3-x^2-x+3

232

336

Посмотреть ответы 2

Ответы на вопрос:

Белка456

Алгебра

4,5(21 оценок)

на

а) функция возрастает на всём промежутке, точек экстремума, соответственно, нет;

б) находишь производную (2х+4), приравниваешь её нулю, 2х+4=0, х=-2 - точка экстремума, подставляешь в уравнение производной пробные значения, при значениях меньше -2 ответ будет отрицательным, значит, функция убывает на данном промежутке. при значениях больше -2 ответ будет положительным, значит, функция возрастает на данном промежутке.

в) производная: 3х^2- 2х, приравниваешь нулю, находишь корни квадратного уравнения (-1/3 и 1) (они же будут являться точками экстремума), рисуешь числовую прямую, подставляешь пробные значения в уравнение производной, например -1; 0 и 2 и там (на тех промежутках), где ответ отрицательный- функция убывает, а где положительный- возрастает.

petyasmolin

Алгебра

4,7(16 оценок)

ответ: x²y + y²x

Объяснение:

Свойства степеней :

$\boxed{\begin{minipage}{7 cm} \\ \\$a^{-1}=\dfrac{1}{a} \\ \\a^n\cdot a^m= a^{n+m} \\ \\a^n:a^m= a^{n-m } (a^n)^{m}=a^{n\times m} (ab)^n= a^n\cdot b^n $\end{minipage}}$

Решение :

$\sf \displaystyle (x^{-1}+y^{-1})\cdot\bigg (\dfrac{1}{xy} \bigg)^{-2} = \bigg(\frac{1}{x}+\frac{1}{y} \bigg) \cdot (xy)^2 =\frac{x+y}{\diagup \hspace{-1em}xy} \cdot (xy)^{\diagup \hspace{-0,5em}2} =(x+y)xy=\boxed{\sf x^2y+y^2x}$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.