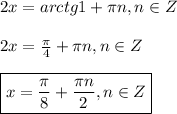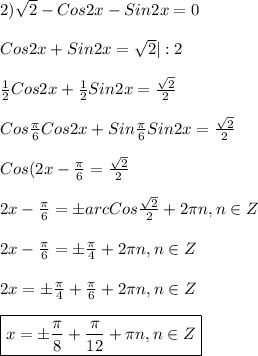Регистрация Спросить otvet5GPT
valdi5p0ch22
23.02.2021 08:17
Алгебра
Есть ответ 👍

Выражение (m^2+9m)+18(m^2+9m)+81 надо представить в виде произведения числа и квадрата многочлена.

140
222
Посмотреть ответы 2

Ответы на вопрос:

кристинка0051
кристинка0051
4,8(17 оценок)
(m²+9m)²+18(m²+9m)+81=(m²+9m+9)²                                 m²+9m+9=0         m1,2=-9/2+/-√81/4 - 9=-9/2+/-√45/4=-9/2+/-3√5/2                                          m1=-9/2-3√5/2=-3(3+√5)/2                        m2=-9/2+ 3√5/2=-3(3-√5)/2         (m+3(3+√5)/2)(m+3(3-√5)/2)=(m²+9m+9)²
РыбкаНемо
РыбкаНемо
4,8(93 оценок)

√2(Sin2x - Cos2x) = Cos4x

√2(Sin2x - Cos2x) = Cos²2x - Sin²2x

-√2( Cos2x - Sin2x) -( Cos2x - Sin2x)(Cos2x + Sin2x) = 0

(Cos2x - Sin2x)(√2 - Cos2x - Sin2x) = 0

1) Cos2x - Sin2x = 0 |: Cos2x , Cos2x ≠ 0

1 - tg2x = 0

tg2x = 1

2x=arctg1+\pi n,n\in Z\\\\2x=\frac{\pi }{4}+\pi n,n\in Z\\\\\boxed{x=\frac{\pi }{8}+\frac{\pi n}{2},n\in Z}

2)\sqrt{2}-Cos2x-Sin2x=0\\\\Cos2x+Sin2x=\sqrt{2} |:2\\\\\frac{1}{2}Cos2x+\frac{1}{2} Sin2x=\frac{\sqrt{2}}{2}\\\\Cos\frac{\pi }{6}Cos2x+Sin\frac{\pi }{6}Sin2x=\frac{\sqrt{2} }{2} \\\\Cos(2x-\frac{\pi }{6}=\frac{\sqrt{2} }{2}\\\\2x-\frac{\pi }{6}=\pm arc Cos\frac{\sqrt{2} }{2}+2\pi n,n\in Z\\\\2x-\frac{\pi }{6}=\pm \frac{\pi }{4} +2\pi n,n\in Z\\\\2x=\pm \frac{\pi }{4}+\frac{\pi }{6} +2\pi n,n\in Z\\\\\boxed{x=\pm \frac{\pi }{8}+\frac{\pi }{12} +\pi n,n\in Z}

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS