Brilliana1999

30.07.2020 01:11

Геометрия

Есть ответ 👍

Сумма углов при основании равнобедренного треугольника равна 100. вычислите: 1-угол при вершине треугольника 2-внешние углы треугольника

269

297

Посмотреть ответы 2

Ответы на вопрос:

Gugulik3

Геометрия

4,4(96 оценок)

угол при вершине угла равен 80, внешные углы равны 130, 130, 80

RomisuRomi

Геометрия

4,4(13 оценок)

ответ: S=96

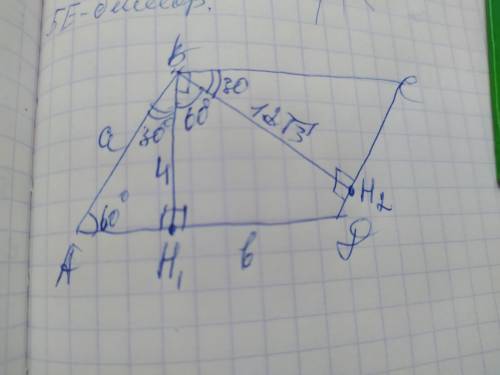
Объяснение: обозначим вершины параллелограмма А В С Д, а его высоты ВН1 и ВН2. Пусть одна его стороны АВ=СД=а, вторые ВС=АД=b. Зная, что площадь параллелограмма - это произведение его стороны и высоты, которая проведена к стороне, составим уравнение согласно формуле площади:

S=b×BH1. Так как площадь будет одинаковой независимо от того какой вариант мы выберем, то:

b×BH1=a×ВН2

4b=12√3a

b=12√3a/4

b=3√3a

Высота ВН1 образует прямой угол 90° также со стороной ВС, поэтому

угол СВН=90-60=30°. Рассмотрим полученный ∆СВН2. Он прямоугольный где ВН2 и СН2 -катеты, а ВС- гипотенуза. Так как сумма острых углов прямоугольного треугольника составляет 90°, то угол С=90-30=60° . В параллелограмме противоположные углы между собой равны, поэтому

угол А=углу С=60°. Рассмотрим полученный ∆ АВН1. Он прямоугольный, где АН1 и ВН1 катеты, а АВ - гипотенуза. Угол АВН=90-60=30°. Катет лежащий напротив него равен половине гипотенузы, поэтому АН=а/2. Составим уравнение используя теорему Пифагора:

АВ²-АН1²=ВН1²

а²-а²/2²=4²

а²-а²/4=16. Здесь ищем общий знаменатель и получаем:

(4а²-а²)/4=16

3а²/4=16

3а²=4×16

3а²=64

а²=64/3

а=√64/3

а=8/√3

Если сторона а=8/√3, тогда

сторона b=8/√3×3√3=24

Теперь найдём площадь параллелограмма, зная его стороны:

S1=8/√3×12√3=96

S2=24×4=96

Найти площадь параллелограмма, если его высоты равны 12√3 и 4, и уголь между ними 60°.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.