Найти координаты концов отрезка,симитричного заданого относительно прямой у=3. координаты отрезка а(-3; 5) и в(4; 1)

154

185

Посмотреть ответы 2

Ответы на вопрос:

iga5

Математика

4,5(88 оценок)

Пусть a(х₁,у₁,z₁) и д(х₂,у₂,z₂)− концы заданного отрезка. 1) в формулы для нахождения координат точки в подставим известные координаты: λ₁=aв/bд=1/2=0,5; хв=(х₁+λ₁х₂)/(1+λ₁) 0=(x₁+0,5х₂)/(1+0,5) x₁+0,5х₂=0 ув=(у₁+λ₁у₂)/(1+λ₁) 3,5=(у₁+0,5у₂)/(1+0,5) у₁+0,5у₂=5,25 zв=(z₁+λ₁z₂)/(1+λ₁) -4=(z₁+0,5z₂)/(1+0,5) z₁+0,5z₂=-6 2) в формулы для нахождения координат точки с подставим известные координаты: λ₂=aс/сд=2/1=2; хс=(х₁+λ₂х₂)/(1+λ₂) -5=(x₁+2х₂)/(1+2) x₁+2х₂=-15 ус=(у₁+λ₂у₂)/(1+λ₂) 6=(у₁+2у₂)/(1+2) у₁+2у₂=18 zс=(z₁+λ₂z₂)/(1+λ₂) 1=(z₁+2z₂)/(1+2) z₁+2z₂=3 3) полученные уравнения соединим в системы и решим: x₁+0,5х₂=0 x₁+2х₂=-15 -1,5х₂=15, х₂=-10, х₁=5 у₁+0,5у₂=5,25 у₁+2у₂=18 -1,5у₂=-12,75, у₂=8,5, у₁=1 z₁+0,5z₂=-6 z₁+2z₂=3 -1,5z₂=-9, z₂=6, z₁=-9 получились координаты концов отрезка а(5, 1, -9) и д(-10, 8,5, 6)

maksim2286

Математика

4,4(17 оценок)

Вот решение ^

ответ: 5/4 = 1 1/4 (пять четвёртых равно одна целая одна четвёртая)

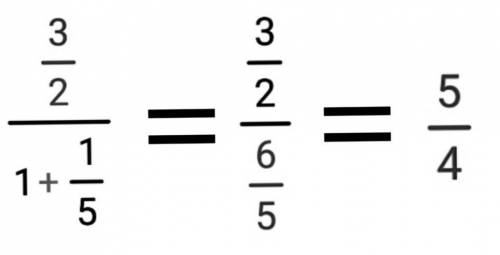
Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.