Найдите значение выражения 7/20 : 0,7 - 4/5 найдите значение выражения 1 5/6-0,5*(-10/3)
133
161
Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Число -5 является арифметическим квадратным корнем из 25?...
 RomanPopov200505.05.2020 11:37
RomanPopov200505.05.2020 11:37 -
Люди, 10 класс ! у меня есть пример решения, только другой пример. у меня a=3....
 ViktoriyaFomina101.01.2021 23:25
ViktoriyaFomina101.01.2021 23:25 -
Номер 6.48 под в) и г) желательно показать на окружности и применить формулы...
 jookyun12.12.2021 13:30
jookyun12.12.2021 13:30 -
Номер 7 под в) и г) желательно показать на окружности и формулы...
 лолкек6623.08.2021 20:24
лолкек6623.08.2021 20:24 -
6.46 в) и г) все расписать в ! подробное решение...
 konfetka751018.07.2020 21:26
konfetka751018.07.2020 21:26 -
Буду чрезмерно , если решите хоть что-то. ...
 kolobok200022.05.2022 13:02
kolobok200022.05.2022 13:02 -
Выражение -5a+(2a+-2a)= 8 класс, 50...
 AnTonnn22117.01.2021 18:56
AnTonnn22117.01.2021 18:56 -
Через две трубы можно наполнить бассей н за 4 часа, а отдельно через первую за...
 6jytu07.02.2022 14:59
6jytu07.02.2022 14:59 -
Выполните действие : (a-2a)+(3a-4a)+(5a-6a)+(7a-8a)+(8a-9a)+(9a-10a)...
 anastasiarazumeeva25.11.2020 00:17
anastasiarazumeeva25.11.2020 00:17 -
1. Составьте одну из возможных формул n-го члена последовательности по первым ее...
 lol104623.10.2021 08:45
lol104623.10.2021 08:45

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

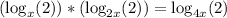
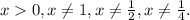
![[*] Formula: \log_{a} (x) =\frac{ \log_{b} (2) }{ \log_{b} (a) }.](/tpl/images/4978/2125/6c007.png)
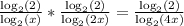
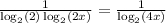
![[*] Formula: \log_{a} (xy)=\log_{a} (x)+\log_{a} (y).](/tpl/images/4978/2125/c3242.png)
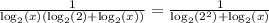
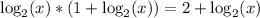
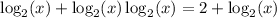
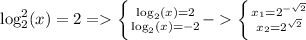
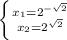 все сходится.
все сходится.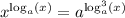
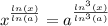
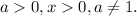
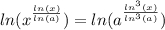
![[*]Formula:ln(x^{y} )=y*ln(x).](/tpl/images/4978/2125/86457.png)
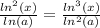
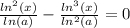
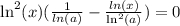
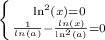
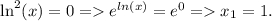
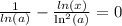
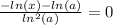 | *
| * 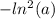
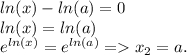
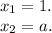 все сходится.
все сходится.